@felixmerk Das Problem ist sich das Ganze 4-dimensional vorzustellen, da wir uns Dimensionen immer nur räumlich vorstellen. Unbewusst gehen wir dagegen ganz gewohnt damit um. Kleines Beispiel:
Wenn wir uns mit jemandem verabreden machen wir einen Ort und eine Zeit aus. Ohne Zeit wird es aber schwierig (Kennt ja jeder: Samstag nächste Woche ich dachte diese Woche mmh grmmpf
;) ). Wenn wir das physikalisch korrekt machen sagen wir wir treffen uns am Ort [x y z] um die Zeit [t]. Also 4 Angaben sind nötig sonst ist die Gefahr groß das man sich verfehlt. Ein erster Hinweis das unsere Zeit aus 4 Dimensionen besteht.
Aber man kann sich das noch besser überlegen:
Anderes Beispiel sind die Flachländer:
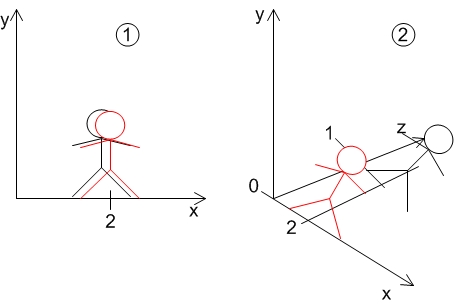
Stellen wir uns vor es gäbe nur zwei Raumdimensionen x und y, dann wäre es unmöglich das 2 Leute am Ort x = 2 und y = 0 stehen (Bild 1). Für die Flachländer geht das einfach nicht. Wenn sie aber herausfinden das es doch irgendwie geht, dann muss es eine dritte Dimension geben und für uns ist das auch nachvollziehbar (Bild 2).
Beliebig viele Leute könne auf x=2 y=0 stehen, der eine ist dann eben auf den Koordinaten x = 2 y = 0 z = 0, der andere auf x = 2 y = 0 z = 1.
Und genau das kennen wir ja auch: Beliebig viele Leute können auf demselben Kinoplatz sitzen, nur eben "nicht" gleichzeitig. Das heißt, wir bekommen zu den Koordinaten x, y, z noch die Koordinate t hinzu. Steht der eine auf x=2 y=0 z=0 kann der andere das auch, nur muss bei ihm dann die Koordinate t dann anders sein z.B. t = 5 --> 1 steht bei x= 2 y=0 z = 0 t=0 hat der andere
eben x=2 y=0 z=0 t=1. Also es gibt 4 Dimensionen.
Das einzige was sich jetzt etwas schwieriger vorzustellen ist, dass Raum und Zeit dasselbe sind, die sogenannte 4-dimensionale Raumzeit. Einstein hat jetzt nur gesagt wir bewegen uns mit konstanter Geschwindigkeit durch diese Raumzeit, nämlich mit c.
Leider ist das im Alltäglichen etwas schwer nachzuvollziehen da wir Geschwindigkeit immer nur auf die Raumdimension x,y,z bezogen sehen. Daher jetzt dieses Schaubild:
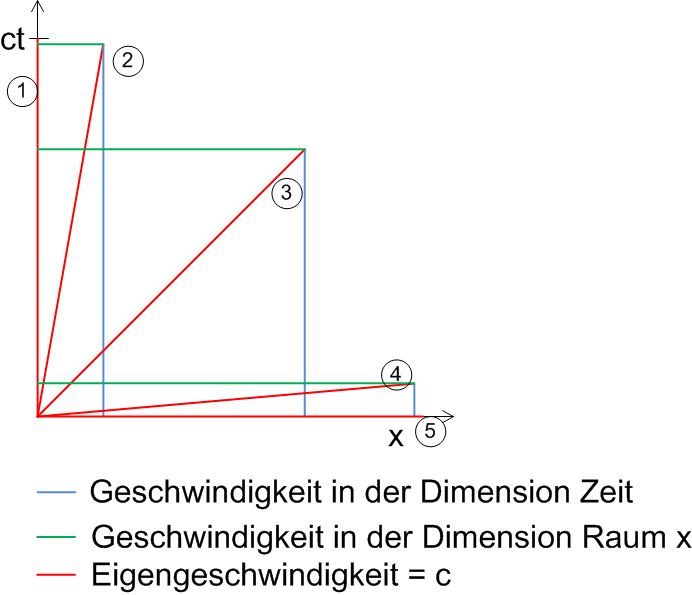
Der einfach halt halber sind hier die Dimensionen y und z weggelassen. Aber zweidimensional reicht auch. Kurze Erklärung zu den Farben.
Sich selber sieht man immer im Raum stehen. Was heißt das: Für dich vergeht die Zeit immer gleich schnell. Das heißt du selber sitzt immer auf der roten Linie und bewegst dich mit c durch die Dimension Zeit. (Man kann sich das gut vorstellen: Man kann zu sich selber keine Geschwindigkeit im Raum messen. Man kann immer nur sagen ich bewege mich mit x km/h zu irgendetwas. Wenn man die Augen zumacht und keinerlei Kraft spürt, kann man unmöglich sagen man bewegt sich mit irgendeiner Geschwindigkeit oder in irgendeine Richtung)
Jemand der sich relativ zu dir bewegt wechselt, für dich den Ort. Das was wir alltagsprachlich als Geschwindigkeit einem Objekt zuordnen ist somit die güne Linie (parallel zur Dimension x). Da sich aber jeder immer mit konstanter Geschwindigkeit c durch die Raumzeit bewegt sieht man, dass dessen Geschwindigkeit für uns in der Zeitdimension verlangsamt ist (blaue Linie). Dazu nun die Beispiele:
Geschwindigkeiten in der Dimension Zeit: rote + blaue Linie
Geschwindigkeiten in der Dimension Raum x: grüne Linie
Du siehtst nun jemanden an die vorbeifliegen. Dafür die 5 Beispiele:
(die vertikale rote Linie ist deine Zeitgeschwindigkeit)
1. Derjenige steht relativ zu dir. D.h die Bewegung über den Ort ist 0 (grüne Linie ist 0). Seine Zeit siehst du genauso schnell vergehen wie deine. Seine blaue Linie ist genau gleich lang wie die rote.
2. Du siehtst jemanden mit geringer Geschwindigkeit an dir vorbeifliegen (kurze grüne Linie). Seine Zeit (blaue Linie) siehst du etwas langsamer vergehen als deine (blau ist etwas kürzer als deine senkrechte rote Linie)
3. Jetzt fliegt der andere schon mit ordentlicher Geschwindigkeit an dir vorbei (grüne Linie wird länger). Dafür siehst du seine Zeit immer langsamer vergehen. Blaue Linie ist wesentlich kürzer als deine rote vertikale Zeitlinie
4. Der andere nähert sich der Lichtgeschwindigkeit in der Dimension x (grüne Linie wird annähernd so lang wie die rote.) Dafür wird die blaue umso kürzer.
Du siehst denjenigen zwar nun richtig schnell an dir vorbeifliegen auf der x-Achse, dafür siehst du aber seine Zeit richtig langsam vergehen (Die blaue Linie ist nun wesentlich kürzer als deine rote senkrechte)
5. Wäre es möglich jemanden auf LG zu beschleunigen hätten wir Fall 5 (grüne Linie gleich lang wie die rote Linie). Das Problem ist nun für dich verschwindet die blaue Linie. Du würdest feststellen bei ihm steht die Zeit still( blaue Line = 0). Das witzige er würde dasselbe von dir behaupten.
Ich hoffe das mach es etwas verständlicher. Mir hat dieses Diagramm sehr geholfen.
kuno7 schrieb:Verstehe immer noch nicht was du meinst. 100m massives Gestein stellen doch für ein Neutrino kein Hinderniss dar, egal ob das nun künstlich ist oder natürlich.