Umgedrehte Kugel

@mandelbaum
Ja also wie gesagt, ich gehe davon aus (Philosophisch), dass sich solch eine Oberfläche pendantisch (im Kontext) verhält, will man auf einen Berg steigen, so müsste es Berg ab gehen, wie eben das Tachyon beim verringern seiner Geschwindigkeit, grosser wird und Energie verliert.

@Radix

also "pendantisch" gibts nicht

und philosophisch betrachtet kommt wohl der Link am nächsten:

http://books.google.de/books?id=2Ajbx2M80gkC&pg=PA48&lpg=PA48&dq=antikugel&source=bl&ots=x4AXoSYs4B&sig=4qJ12yOwzHSw2fpnFkR6XKM4VyU&hl=de&ei=fPfqSaqtNomI_Qa-j43jAw&sa=X&oi=book_result&ct=result&resnum=3#v=onepage&q&f=false

@mandelbaum

pendantisch gibts schon, nur in einem anderen Sinn, deshalb ja (im Kontext)

Philosophisch betrachtet am nächsten kommt immer nur das, was man selbst als das der Wahrheit am nächsten kommende erkennt.

@mandelbaum

pendantisch gibt's nicht, mein Fehler.

@Radix

vielleicht meinst du pedantisch?
falls du kein wörterbuch besitzt -
http://www.wie-sagt-man-noch.de/synonyme/pendantisch.html

mich würde mal interessieren wie die Illustration mit einer
Kugel aussehen würde ; )
http://rneumann.name/index.php?content=hyper2

@mandelbaum

mandelbaum schrieb:falls du kein wörterbuch besitzt -

Ich habe Internet!

mandelbaum schrieb:mich würde mal interessieren wie die Illustration mit einer
Kugel aussehen würde ; )

Eine vierdimensionale Kugel...naja, eine Sphäre in einer massiven Kugel. Würd ich auch mal gerne sehen.

Ist es sowas?

Trotzdem seltsames Video.

Sphere Inside out Part - II

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

@ pumpkin:
Ich habe den Thread noch einmal angefangen, weil ich mir selbst schon lange die Frage stellte, aber erst in letzter Zeit danach im Netz gesucht habe. Eure Diskussion war ja vor etlichen Monaten eingeschlafen und wenn innerhalb der bekannten Gruppe keiner mehr darüber diskutieren will, weil alles gesagt wurde, kommt eben irgendwann jemand von außerhalb und macht weiter. Daher fangen Neulinge wohl oft alte Threads neu an.

Ich habe noch darauf geantwortet, weil ich wissen wollte, wie die Forenmitglieder das bewerten und eventuell widerlegen. Ich habe im Studium ständig mit Oberflächenvergrößerung- und Spannung zu tun und so interessiert es mich, was eigentlich das Gegenteil dazu ist. Ich denke, man muss erst die Extreme kennen, um einen Sachverhalt wirklich begreifen zu könenn.

das gegenstück zu einer kugel ist ein loch wo die kugel rein passt

Bildlich gesprochen meinte ich es etwa so (hoffe der Anhang wird angezeigt), nur mit unendlich vielen Ebenen innerhalb der Kugel, statt nur mit vieren:

mandelbaum schrieb:mich würde mal interessieren wie die Illustration mit einer
Kugel aussehen würde ; )

Vielleicht so:

https://www.youtube.com/watch?v=R_w4HYXuo9M (Video: How to Turn a Sphere Inside Out)

Aber diese Videos zeigen nur, wie man die Innenseite nach außen bekommt, nicht wie das Gegenteil einer Kugel aussieht. Wenn die Innenseite außen ist wird sie zur Außenseite und alles ist wie zuvor, nur dass die Oberfläche nun vielleicht anders aussieht.

Das Problem liegt im Grunde nur im Gegenteil einer einzigen Kugel. Im Verbund sind die Zwischenräume der Kugeln leicht auszumachen. An Kreisen (also 2-dimensional) veranschaulicht ähnelt der Zwischenraum von 6 aneinandergelegten Kreisen ringförmig um den Hohlraum einem Sechseck mit nach innen gewölbten Außenflächen. Bei 5 Kreisen sieht es aus wie ein Fünfeck usw. bis zu drei Kreisen. Bei zwei Kreisen ist das ganze schon unendlich, weil man eine Aneinanderreihung von mindestens drei Kreisen (oder vier Kugeln) haben muss, um eine Fläche und damit einen Zwischenraum definieren zu können. Genauso, wie man mindestens drei Eckpunkte für die einfachste Fläche des Dreiecks braucht (bzw. 4 für eine dreiseitige, dreidimensionale Pyramide). Bei einer Kugel schließlich gäbe es gar keinen Zwischenraum, sondern alles andere außerhalb der Kugel wäre das Gegenteil.

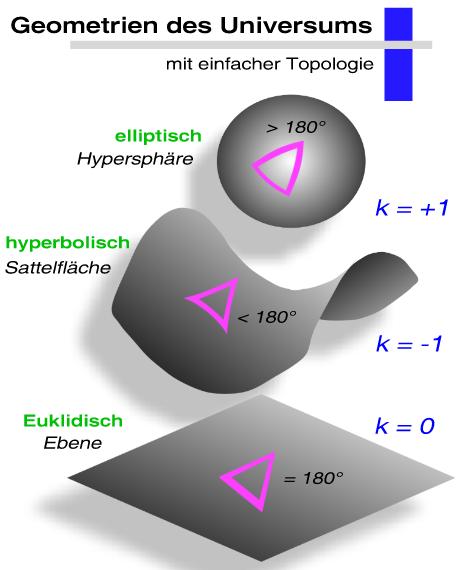
Was ich mir außerdem noch einfällt: Die Geometrien des Universums werden häufig auf drei mögliche Formen festgelegt: Die Kugel, die Fläche (euklidisch) und den Sattel (hyperbolisch) (siehe Anhang). Wenn man Wölbung betrachtet, wäre danach der Sattel das Gegenteil der Kugel, auch wenn ich mir das selbst nicht bildlich vorstellen kann, aber praktisch wie die Oberfläche aufgeklappt und da sie gewölbt ist, bildet sie keine Fläche sondern eben einen Sattel.

Hallo Leute

also, ich stelle mir unter "das Gegenteil einer Kugel" sowas wie ein Sattel vor. Etwa wie ein negatives Abdruck von einer Kugel, wobei das dann nur der Abdruck von der hälfte der Kugel wäre. Um sich ein negativ Abdruck von einer ganzer Kugel vorzustellen müsste man sich also ein "nach außen hin offnes Donut" vorstellen.
Hier ein Beispiel aus der Physik:

http://theory.gsi.de/~vanhees/faq/kosmo/img12.png (Archiv-Version vom 01.04.2007)

Greets

@snafu

Geniales Video, hat mich Spaß gemacht.

Eine Kugel ist doch perfekt. Der perfekte Raum. Zumindest in der Kunst wird das so gesehen. Und etwas perfektes hat kein Negativ. Vielleicht frei interpretiert, aber immerhin logisch :P

@federa
Auf molekulare Ebene hat alles Ecken und Kanten, auch eine Kugel..
Negativ war hier nicht im Sinne von Polarisierung gemeint sondern eher wie bei Fotos, dH eine Introversion..

Hehe, als ich den Threadtitel las schoss mir gleich diese Form in den Kopf:



Ist natürlich blödsinn.....wenn man sich aber eine Kugel vor sich vorstellt wie man sie mit den Händen in der Mitte auseinanderzieht......könnte man sich vorstellen dass sie sich so "umstülpt" dass sie wie ein Diabolo aussieht ^^

mfg

Das Gegenteil einer Kugel ist für mich ganz klar ein Doppeltrichter. Es ist genau das, was im Weltraum als schwarzes Loch bezeichnet wird.

@Missterra

Doppeltrichter?
Original anzeigen (0,2 MB)

....

Mal ernsthaft
Ich glaub du verwechselst schwarze Löcher und Wurmlöcher

Loch im Apfel:


...

pöser schwarzer Vielfraß: