@delta.m  delta.m schrieb:Eine Formel wäre hilfreicher gewesen ....
delta.m schrieb:Eine Formel wäre hilfreicher gewesen ....
Eine Formel für ein Swing-By von einem Photon zu finden wird wahrscheinlich eine ordentliche Herausforderung. Eine lupenreine Herleitung kann ich dir nicht liefern aber einen Versuch ;-)
Zuerst mal ein Argument von Florian Freistetter was er unter Swing-by einer Sonde versteht:
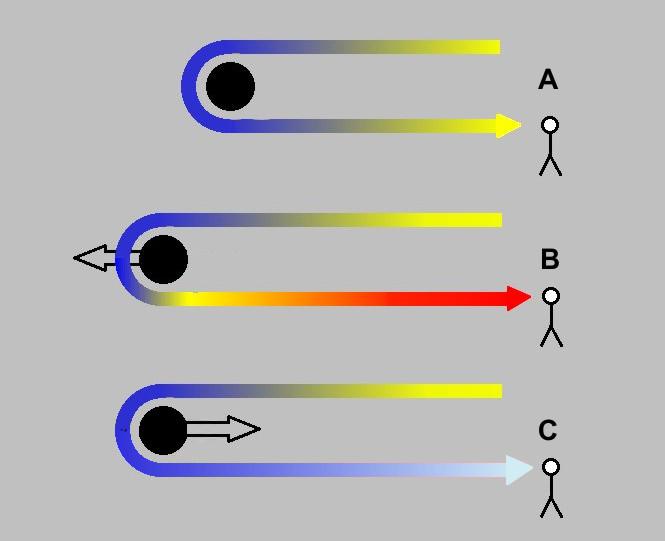
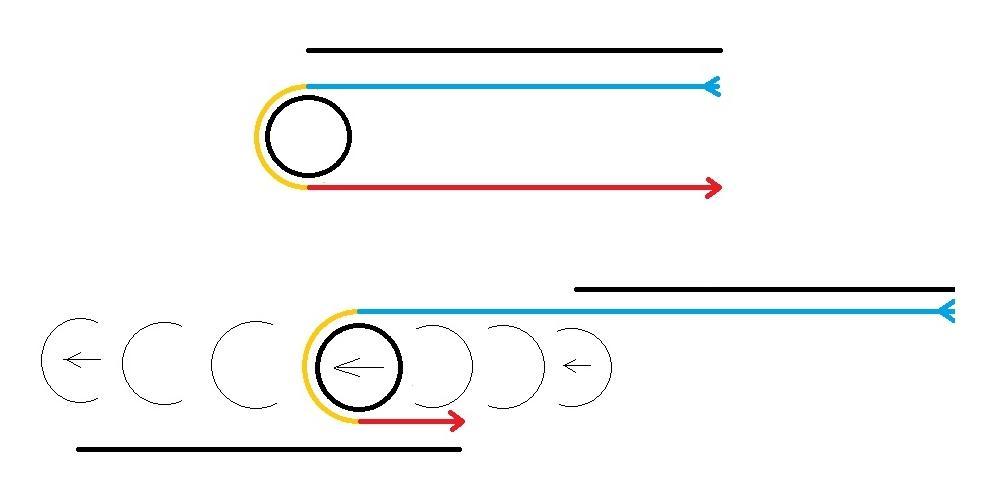
Wenn sie beispielsweise sehr nahe am Jupiter vorbei fliegt, wird sie das nicht einfach unbeeinflusst tun – ihre Bahn wird verändert werden. Aus Sicht des Jupiters findet dabei tatsächlich nur eine Ablenkung statt. Die Raumsonde fliegt nach dem Vorbeiflug in eine andere Richtung als vorher, aber immer noch mit der gleichen Geschwindigkeit. Der Jupiter selbst steht aber nicht still sondern bewegt sich selbst um die Sonne. Und wenn man das ganze aus der Sicht der Sonne betrachtet, hat sich nach dem Vorbeiflug am Planeten nicht nur die Flugrichtung der Sonde verändert sondern auch ihre Geschwindigkeit.
Hier der lohnende Link zum Blog!oder
Wikipedia: Swing-by#PrinzipDer fett markierte Teil ist entscheident, den er liefert einen wichtigen Hinweis: Ein Swing-by sieht aus dem Ruhesystem des Planeten aus wie eine einfache Ablenkung. Das kennen wir auch von Licht nämlich den Gravitationslinsen, die ändern nämlich auch die Richtung des Lichtstrahls. Der Impuls von Licht zeigt sich aber im Gegensatz zu massebehafteten Objekten nicht in der Geschwindigkeit des Photons sonder in dessen Frequenz bzw. Wellenlänge:
p = \frac{h}{\lambda}
Nun wissen wir das Licht von massebehafteten Objekten abgelenkt wird, wie sieht dann die Sache aus wenn Licht von bewegten massebehafteten Objekten abgelenkt wird? Dann müssten wir, in Einklang mit dem Swing-by und obiger Argumentation einen Frequenzshift erwarten, da sich aus unserer Sicht der Impuls ändert.
Das ist ein Punkt den man nachschauen kann. Zuerst habe ich nach
gravitational lens distance dependent redshift geschaut und nichts gefunden. Die Idee dahinter war das weiter entfernte Linsen eine höhere Relativgeschwindigkeit aufweisen und dadurch einen zusätzlichen Impuls bzw. eine Frequenzänderung herbeirufen.
Ich habe keine belastbaren Publikationen gefunden. Eine Publikation die der Thematik vielleicht "am Nächsten" kommt ist diese hier:
On aberration in gravitational lensingDaraus:
It is known that a relative translational motion between the deflector and the observer affects gravitational lensing. In this paper, a lens equation is obtained to describe such effects on actual lensing observables. Results can be easily interpreted in terms of aberration of light-rays. Both radial and transverse motions with relativistic velocities are considered. The lens equation is derived by first considering geodesic motion of photons in the rest-frame Schwarzschild spacetime of the lens, and, then, light-ray detection in the moving observer's frame. Due to the transverse motion images are displaced and distorted in the observer's celestial sphere, whereas the radial velocity along the line of sight causes an effective re-scaling of the lens mass.
Allerdings bin ich mir nicht sicher ob das eure Frage klärt, aber wenn ich mir die Mathematik in der Publikation anschaue, bin ich mir sicher das eine Formel wie sie sich
@delta.m vorstellt in der Art aussehen müsste: Man müsste sich das Linienelement im einfachsten Fall einer Schwarzschild-Metrik (z.B. für die Erde) für ein Photon berechen aus Sicht der ruhenden und der bewegten Masse und dann schauen ob sich Frequenzunterschiede ergeben. Mein Fazit dahingehend das ich keine Literatur dazu gefunden habe ist dass der Effekt entweder (i) nicht exisitert bzw. schon nicht viel SInn macht, (ii) bisher nicht nachweisbar (wobei es dann trotzdem theoretische Ausarbeitungen geben müsste/könnte) ist oder (iii) ich nur schlampig gesucht habe.
PS: Eine ähnliche Frage gab es schonmal hier:
https://physics.stackexchange.com/questions/368863/how-does-gravitational-lensing-affect-red-shift