e^x wächst schneller als jede Potenzfunktion
31.01.2011 um 17:02^ geht schneller!chen schrieb:Wenn ihr Superscript benutzt, könnt ihr auf die ^ - Zeichen verzichten.
Und so kompliziert waren die Exponenten ja nun wieder auch nicht, aber ok... wenn du alter Herr das dann besser lesen kannst, mach ichs eben so :D
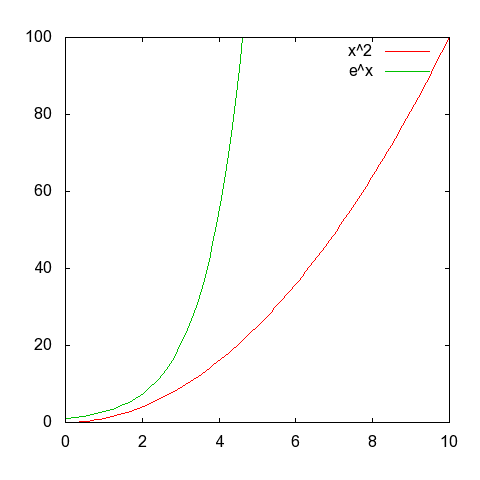
Das Standardbeispiel wäre natürlich x² und ex.Halbvampirroni schrieb:Einen Grafen zur veranschaulichung oder so?
kann man da irgendein Beispiel nehmen?
x³ und ex ist noch eine Spur interessanter, da dort die Potenzfunktion für kleine Werte (~ 1,85 < x < 4,54) einen höheren Funktionswert besitzt als die Exponentialfunktion.
Noch größere Parameter für den Exponenten verschieben den zweiten Schnittpunkt weiter nach oben, das wird dann schnell unübersichtlich.
Vielleicht wird so klar, was ich meine:
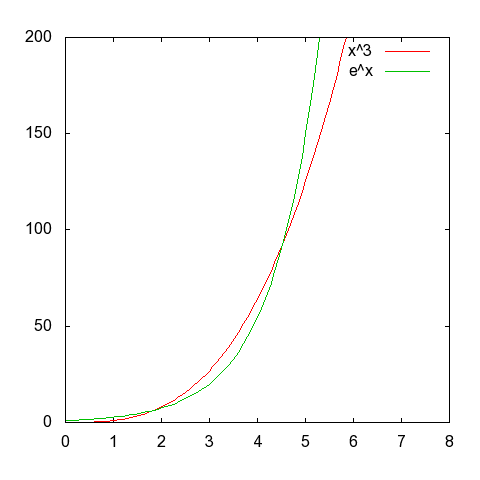
Für x4 hat der obere Schnittpunkt dann einen y-Wert von ~ 5500, das ist auf einer Grafik nicht mehr gut darstellbar.