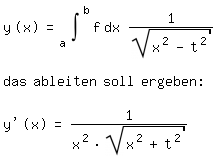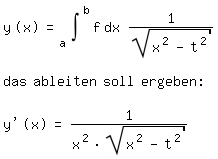@Tommy137 Jo musste kurz wech ^^
Also noch mal langsam
dz/du = dz / [sqrt{u²(z)-p²}]
Quotientenregel: u/v = [u'v - v'u] / v²
Kettenregel u(v(x)) = u' (v(x))*v'(x)
Ableitung der Wurzel mit Kettenregel:
sqrt{u²(z)-p²} = - 1/2 * 2u(z) / [sqrt{u²(z)-p²}] den Ausdruck nenn ich mal T
Jetzt dz / [sqrt{u²(z)-p²}] mit Quotientenregel
u' = 0
v = sqrt{u²(z)-p²}
v' = T
u(z) = [Integral über z1 bis z2 von]
[0* sqrt{u²(z)-p²} + T] / u²(z)+p² = { 1/2 * 2u(z) / [sqrt{u²(z)-p²}] } / [u²(z)-p²]
2 kürzt sich ja schön weg:
u(z) / [sqrt{u²(z)-p²}] / [u²(z)-p²] oder halt in 2 Brüchen
dz/du = u(z)/[sqrt{u²(z)-p²}] * 1/[u²(z)-p²]
den Ausdruck da den will ich nur vereinfacht haben, sodass rauskommt
dz/du = 1/[u²(z)*sqrt{u²(z)-p²}]
Ich weiß jetzt net ob ich mit ner Substitution dahin komme, aber eigentlich müsste ja einfach nur kürzen, erweitern etc zum Ziel führen ...
du kannst ja vereinfacht u²(z)+p² = x nehmen dann steht dann halt da:
dz/du = u(z) / sqrt(x) * 1/x und am Ende irgendwann hoffentlich
dz/du = 1 / [u(z) * sqrt (x)]
oder ganz einfach:
u/sqrt (x) * 1/x = 1 / [u*sqrt(x)]