Tierbeine-Paradoxon

RayWonders schrieb:X*1000 > X*4

das ist mal unendlich wahr :Y:

vielleicht kann man mit der unendlichkeit prüfen ob etwas wahr ist oder nicht

Mousetrap schrieb:Gäbe es mehr Tausendfüßerbeine als Katzenbeine, wenn es UNENDLICH viele Tausendfüßer und UNENDLICH viele Katzen gäbe?

damit sie alle platz haben muss das universum grenzenlos sein

Spoiler
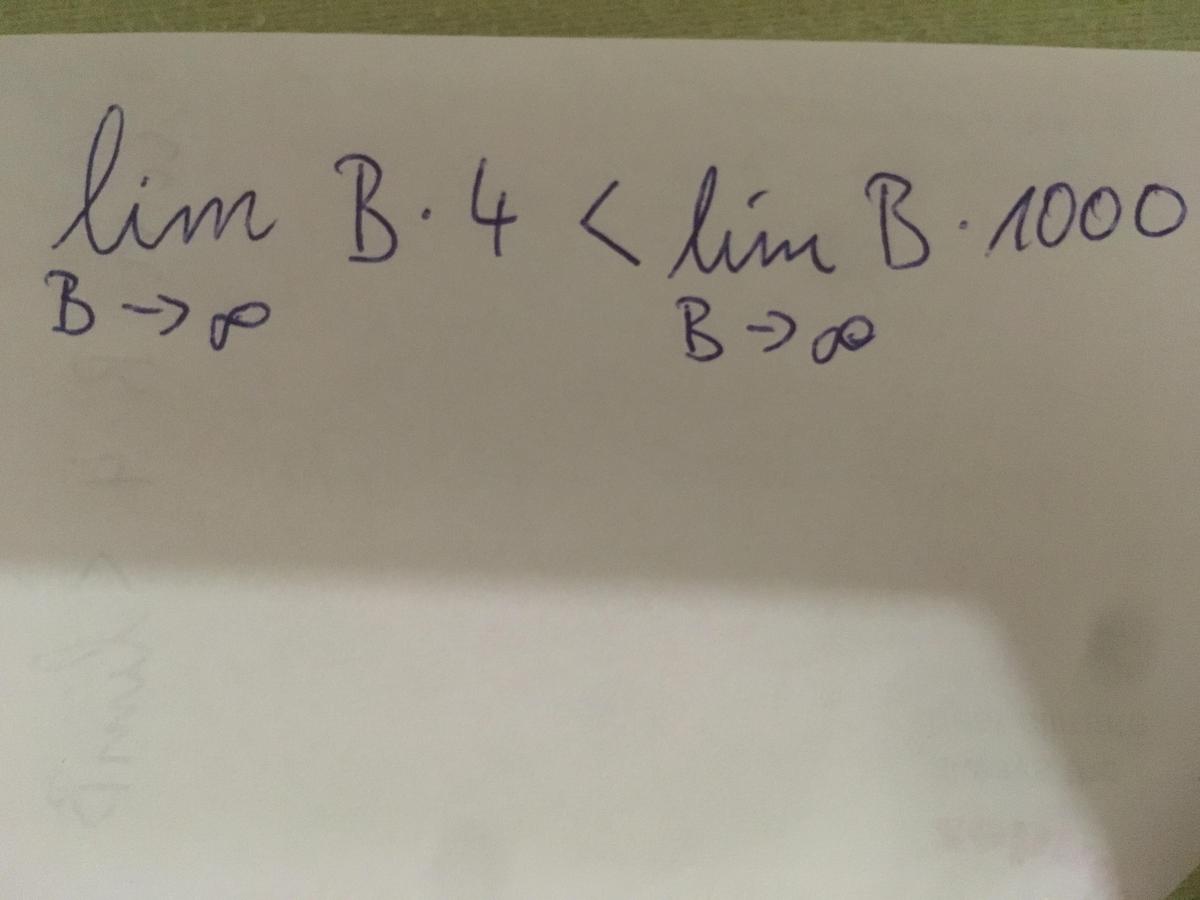Original anzeigen (0,8 MB)

Sieht so aus wie ja. Aber die Frage ist natürlich wer schneller unterwegs ist mit seinen unendlich Beinen. Die Katzen oder die Insekten @Mousetrap ?

aber wenn du die zeit anhälst
die bezugs systeme sind raum und existenz > die form natürlich, muss bleiben und du darfst keinen ausschnit aus der matrix einzeln betrachten, sehe das komplette alles :P

ohne bezugssystem, kann man unendlich viele bezugssysteme in betracht ziehen ;)

sagen wir die zeit ist nicht konstant mit der du die beine zählst, dann kann man beide gleich schnell zählen, deshalb anhalten und alle kennen die in dem moment exestieren.

asserdem kann man nicht die anzahl der beine von der anzahl der tiere trennen, sie sind alle unendlich, wären meine ich , also wenn

Bettman schrieb:Aber die Frage ist natürlich wer schneller unterwegs ist mit seinen unendlich Beinen.

dafür brauchen die aber eine unedliche Fläche? warum das?

Hm, unendlich viele Tausendfüßler hätten unendlich viele Beine.
Unendlich viele Katzen hätten auch unendlich viele Beine.

Also gäbe genauso viele Tausendfüßlerbeine wie Katzenbeine:
Jeweils unendlich viele.

Um die Unterbringung der Viecher mach ich mir aber lieber keine Gedanken.
óò

@Dr.Murks
Und wo dürfen dann meine Beine noch hinlatschen?
Aber das Prinzip.....

@Mousetrap

Um diesen kleinen "Missstand" mal aufzuerfragen..

Wenn diese beiden Kategorien alles füllen würden, was unser Geist zu bieten hat, also 100% von allem, wo sind wir dann noch?

Ist da nicht schon längst das "Paradoxon" erreicht?

Mit anderen Worten....

Ihr macht hier einen absoluten Denkfehler!

Unendlichkeit gegen Unendlichkleit aufzuwiegen, ist gleich null!

Da ist es egal, welche Spezies dabei genannt wird.

Katze, Tausendfüssler sind dabei nur gedankliche Konstrukte.

Ihr Schlaumeierse..

Wenigstens hat sich @Dr.Murks noch Gedanken dazu gemacht!!

Alle anderen sollten sich schämen, das "Smartphone" sowas von zu unterstützen..

Habt ihr denn gar keinen Respekt mehr, vor der Logik eurer "Vor-Generationen"?

Das ist alles Murks.

Unendlich ist nunmal unendlich.

Da brauch man auch nicht anfangen zu zählen etc.

TerracottaPie schrieb:Das ist alles Murks.

Unendlich ist nunmal unendlich.

Da brauch man auch nicht anfangen zu zählen etc.

bei mir hats an der Mathematik gehapert, kann man 2 unendlichkeiten in bezug bringen? ohne die beine von den körpern zu trennen?
kennst du dich da mathematisch aus?

Erinnert mich an dieses Gedankenexperiment :D

All diese Möglichkeiten sind nicht wirklich paradox, sondern widersprechen nur der Intuition. Es ist schwierig, sich eine Vorstellung von unendlichen „Zusammenfassungen von Dingen“ zu machen, da ihre Eigenschaften sich sehr unterscheiden von denen gewöhnlicher, endlicher „Zusammenfassungen von Dingen“. In einem Hotel mit endlich vielen Zimmern ist die Anzahl der Zimmer mit ungerader Nummer offenbar kleiner als die Anzahl aller Zimmer, sobald es mindestens ein Zimmer mit einer geraden Nummer gibt. In Hilberts Hotel, das treffenderweise „Grand Hotel“ genannt wird, ist die „Anzahl“ der Zimmer mit ungerader Nummer jedoch in gewissem Sinne „genauso groß“ wie die „Anzahl“ aller Zimmer. Mathematisch ausgedrückt wird das so: Die Mächtigkeit der Teilmenge der Zimmer mit ungerader Nummer ist gleich der Mächtigkeit der Menge aller Zimmer. Man kann unendliche Mengen über die Eigenschaft definieren, eine gleichmächtige echte Teilmenge zu haben. Die Mächtigkeit abzählbarer Mengen wird {\displaystyle \aleph _{0}} \aleph _{0} („Aleph 0“) genannt.

Wikipedia: Hilberts Hotel

Kann man also sagen, die Menge der Katzenbeine gleich groß der Menge der Tausenfüßerbeine ist? :ask:

@CriticalRush

Ist doch ganz simpel.

Wir haben unendlich viele Tausendfüßer.

Diese haben unendlich viele Beine.

Wir haben unendlich viele Katzen.

Diese haben unendlich viele Beine.

Von beiden Beinen haben wir unendlich viele.

TerracottaPie schrieb:Ist doch ganz simpel.

...

Von beiden Beinen haben wir unendlich viele.

das denke ich auch, aber könnte man vielelicht mit der unendlichkeit einen beweis dafür finden ob mathemakti einen fehler hat oder auch nicht?

der begriff ist so schwammig, weil man den halt relativ benutzt wenn man kein mathematiker ist, aber wenn Mathematiker auch die unendlichkeit nutzen, ? dann würde das vielleicht echt was zum verständniss beitragen

CriticalRush schrieb:der begriff ist so schwammig

Ist er an sich nicht.

Viele haben einfach nur ein Problem mit der Imagination dieses Begriffes.

Mathematiker bin ich nicht. Und worauf du abziehlst ist mir auch nicht klar.

Mich wundert es, dass so viele für die erste Antwort gestimmt haben.

TerracottaPie schrieb:Ist er an sich nicht.

beispiel: wie lange läuft die installation beim hängengebliebenem PC wenn keiner eingreift? unendlich :D

TerracottaPie schrieb:Mathematiker bin ich nicht. Und worauf du abziehlst ist mir auch nicht klar.

ich interessiere mich ob es mathematische unendlichkeits sätze gibt