2ter Hauptsatz Kugelstoßkaskade

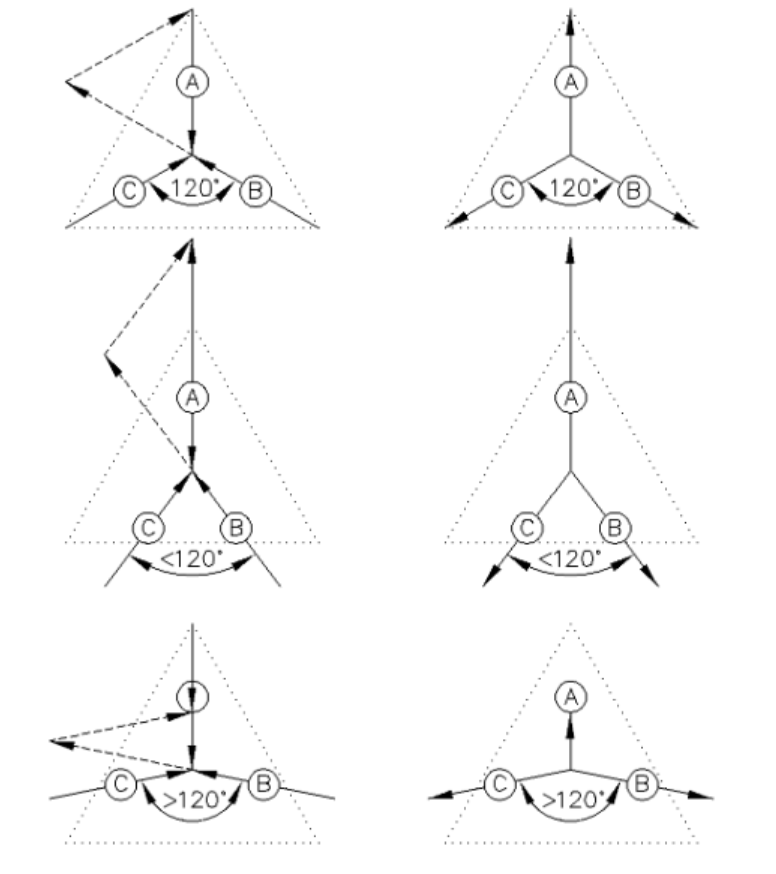
1



2





Kugelstoßkaskade


Fasst man die Entropie nicht nur als eine rein statistische Größe, sondern in
ihrer allgemeinsten Form, als ein Ordnungsmaß für Potentiale auf, dann lässt
sich in einem 3 Körperversuch sehr schön zeigen, worauf es beim Auf- und
Abbau von Ordnungen wirklich ankommt.
Betrachten wir einen Stoßversuch mit drei Kugeln A, B und C gleicher Masse, gemäß der Abb. 1. Diese bewegen sich mit gleicher Geschwindigkeit und daher auch gleichem Impuls aufeinander zu.
Bei einem Winkel von jeweils 120° zwischen den Kugelbahnen zeigt eine einfache Addition der Vektoren, dass die Summe aller Impulse Null ergibt. Daraus folgt, dass sich die 3 Kugeln nach dem Zusammenstoß wieder mit derselben Geschwindigkeit auf ihrer ursprünglichen Bahn vom Mittelpunkt entfernen. Es hat sich zunächst nichts geändert.

Verringern wir nun den Winkel in dem System derart, dass zwischen den zwei Kugeln B und C ein kleinerer Winkel, von unter 120º herrscht, ergibt die Vektoraddition vor dem Stoß einen positiven Summenvektor in Richtung der dem spitzen Winkel gegenüberliegenden Kugel A. Die Impulsübertragung erfolgt daher nicht mehr symmetrisch und die Kugel A wird sich nach dem Stoß schneller bewegen, während die beiden Kugeln B und C zum Erhalt des Gesamtimpulses entsprechend langsamer werden. Umgekehrt erfolgt für einen Winkel von größer 120° eine Aufteilung der Energie auf die Kugeln B und C, was dem normalen Fall der Energiezerstreuung entspricht.
Obwohl bei einem idealen Stoß in der Summe die kinetische Energie des
Gesamtsystems immer noch gleich geblieben ist, wurde dennoch innerhalb des Systems der 3 Kugeln eine Potentialdifferenz zwischen der Kugel A und den Kugeln B, C erschaffen, die vor dem Stoß nicht vorhanden war.
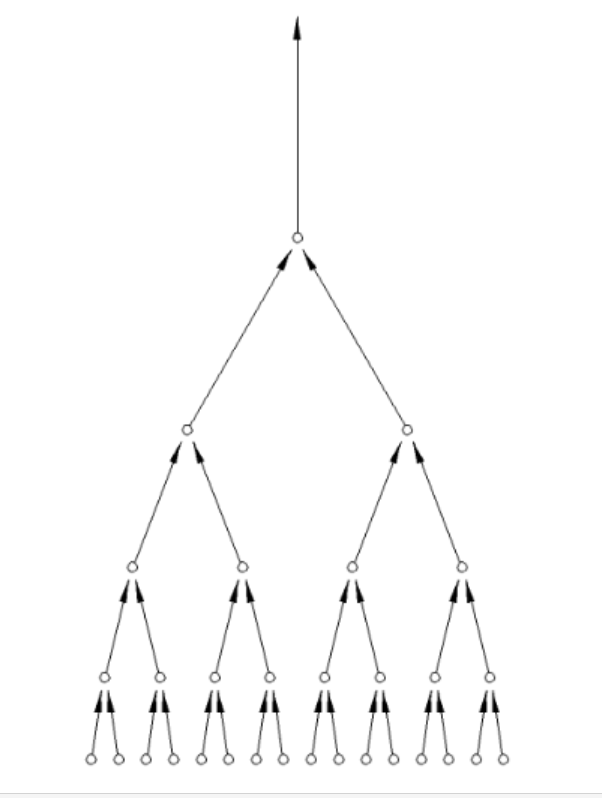
Stellen wir uns für den Aufbau eines thermischen Potentiales nun viele parallele Dreierkugelsysteme, gemäß der Abb. 2 vor, in denen zeitgleich in derselben Weise Kinetik umgeschichtet wird. Greifen wir daraus die jeweils beschleunigten Kugeln heraus und führen sie kaskadenartig in derselben spitzen Winkelanordnung immer weiter zusammen.
Es lässt sich leicht deduzieren, dass nach einiger Zeit die Energie von immer
weniger Masseträgern immer höher wird, während immer mehr Kugeln ihre
Kinetik abgeben. Da unser Beispiel im Prinzip von der Größe der Kugeln unabhängig ist, lässt sich daraus der Schluss ziehen, dass es mittels geeigneter, geometrischer Kaskadenvorrichtung auch möglich ist, aus Feldern ungerichteter Quantenfluktuationen mit hoher Entropie (Moleküle, Elektronen, Neutrinos usw.) Potentiale aufzubauen. Der Schlüssel zur Nutzung sind geometrische Formen, in diesem Fall eine spezielle Dreiecksanordnung, und daher nur eine Frage der Information, aber eben nicht zwingend der Energie.
Dies tangiert die Masse von Körpern derart, dass für die Erschaffung höherer
kinetischer Potentiale, die langsamer werdenden Teilchen durch den Verlust
ihrer Kinetik lokal näher zusammenrücken und dabei in Summe ihre physikalischen Eigenschaften verändern.

Hier schließt sich der Kreis und erklärt, warum viele Stoffe innerhalb eines
ansteigenden Temperaturprofiles, eine Veränderung des Körperwärmewertes
aufweisen.