Ich hatte hier vor Längerem einen ausführlichen
Beitrag über zwei scheinbare Verletzungen der Energieerhaltung im Zusammenhang mit dem
Relativitätsprinzip der klassischen Mechanik gepostet. Einen dritten Fall hatte ich kurz erwähnt, aber nicht näher erläutert. Ich möchte nun auch diesen dritten Fall erläutern, weil ausgerechnet jemand, von dessen naturwissenschaftlich/technischer Kompetenz ich eigentlich sehr viel halte, meint, bei diesem dritten Fall eine Verletzung der Energieerhaltung zu erkennen. Das lässt mich vermuten, dass diese Vorstellung verbreiteter ist, als ich bisher angenommen hatte.
Simon Derricutt, seit langer Zeit einer der bekanntesten Freie-Energie-Kritiker im englischsprachigen Raum, schreibt:
If you apply a force to an object in the lab frame, it accelerates and the accumulated kinetic energy is force times distance and is absolutely equal to the energy used. Energy is conserved.
On the other hand, if you use a rocket (and we'll specify an ideal rocket where the mass loss is negligible and the thrust remains constant for a sufficient time) then the measured thrust is relative to the rocket. The energy use is constant each second. However, the work done (in the lab frame) now depends on the instantaneous velocity, and the accumulated energy depends on 0.5mv² in the lab frame. Oddly, in the rocket's (accelerating) frame of reference the thrust from the rocket does no work at all.
With the rocket, we thus have a situation where the energy used is constant per unit of time, but where the accumulated kinetic energy rises as v². If the rocket goes fast enough, it's producing more kinetic energy in our lab frame that it uses to produce the thrust. That kinetic energy is real.
Where does this extra energy come from?
(Simon Derricutt am 29.03.2022)
Ich beschreibe die grundsätzliche Idee auch nochmal auf Deutsch:
Eine idealisierte Rakete bewege sich über einen gewissen Zeitraum mit einer konstanten Schubkraft fort, die mit einem konstanten Verbrauch an Antriebsenergie verbunden sei. Das sind z.B. für eine Flüssigkeitsrakete unproblematische Annahmen. Der Massenverlust durch die ausgestossene Rückstossmasse sei dabei vernachlässigbar. Diese Annahme ist problematisch, wie sich noch zeigen wird.
Eine konstante Schubkraft bei konstanter Masse führt zu einer laufend linear steigenden Geschwindigkeit, und daraus ergibt sich nach der klassischen Formel
E_{kin}=\frac{1}{2}*m*v^2 eine quadratisch steigende kinetische Energie der Rakete. Es steht also scheinbar einem linearen Verbrauch an Antriebsenergie eine quadratische Zunahme der kinetischen Energie der Rakete gegenüber, was einem Energiegewinn aus dem Nichts entspräche. Wo ist der Fehler?
Die grundlegende Formel für die Schubkraft eines Rückstossantriebs lautet (das Subskript e steht für den englischen Begriff exhaust):
\begin{aligned}
F &= \frac{dm_{\mathrm e}}{dt}*v_{\mathrm e} = \dot{m}_{\mathrm e}*v_{\mathrm e} \\
[8pt]\text{wobei:}&\hphantom{\hspace{80ex}}\\[8pt]
F &= \text{Schubkaft}\\
dm_{\mathrm e} &= \text{Rückstossmasse, die in der Zeit $dt$ ausgestossen wird} \\
dt &= \text{Zeit, in der die Rückstossmasse $dm_{\mathrm e}$ ausgestossen wird} \\
v_{\mathrm e} &= \text{Geschwindigkeit, mit der die Rückstossmasse ausgestossen wird} \\
\dot{m}_{\mathrm e} &= \text{Massenstrom (Masse pro Zeit) der Rückstossmasse} \\
\end{aligned}
Die Beschleunigung der Rakete ergibt sich entsprechend der Formel:
\begin{aligned}
a &= \frac{F}{m} \\
[8pt]\text{wobei:}&\hphantom{\hspace{80ex}} \\[8pt]
a &= \text{Beschleunigung der Rakete} \\
F &= \text{Schubkaft} \\
m &= \text{Masse der Rakete} \\
\end{aligned}
Die Beschleunigung der Rakete ist dabei trotz der konstanten Schubkraft nicht konstant, weil die Masse der Rakete durch den Ausstoss an Rückstossmasse laufend abnimmt:
\begin{aligned}
m &= m_0-\dot{m}_{\mathrm e}*t \\
[8pt]\text{wobei:}&\hphantom{\hspace{80ex}} \\[8pt]
m &= \text{Masse der Rakete} \\
m_0 &= \text{Anfangsmasse der Rakete} \\
\dot{m}_{\mathrm e} &= \text{Massenstrom (Masse pro Zeit) der Rückstossmasse} \\
t &= \text{Zeit} \\
\end{aligned}
Bei einer konstanten Beschleunigung ergibt sich die Geschwindigkeit nach einer bestimmten Zeit entsprechend der Formel:
v = a*t
Da die Beschleunigung der Rakete wegen der abnehmenden Masse aber nicht konstant ist, muss die Geschwindigkeit in diesem Fall mit einem Integral berechnet werden. Ein Integral ist, wie ich in anderem Zusammenhang schon mal geschrieben hatte, in gewissem Sinne eine Multiplikation, bei der sich mindestens einer der Faktoren
während der Multiplikation ändert.
v = \int_0^t a\,dt = \int_0^t \frac{F}{m}\,dt = \int_0^t \frac{F}{m_0-\dot{m}_{\mathrm e}*t}\,dt
Das ist nach Herausziehen des konstanten Faktors F ein einfach zu lösendes Standard-Integral, dessen Lösung man in gängigen
Integral-Tabellen nachschlagen kann:
\begin{aligned}
v &= F * \int_0^t \frac{1}{m_0-\dot{m}_{\mathrm e}*t}\,dt \\
&= F * \left[ -\frac{1}{\dot{m}_{\mathrm e}} * \ln{(m_0-\dot{m}_{\mathrm e}*t)} \right]_0^t \\
&= -\frac{F}{\dot{m}_{\mathrm e}} * \bigg[ \ln{(m_0-\dot{m}_{\mathrm e}*t)} \bigg]_0^t \\
&= -v_{\mathrm e} * \bigg[ \ln{(m_0-\dot{m}_{\mathrm e}*t)} \bigg]_0^t \\
\end{aligned}
Die letztere Umformung ergibt sich aus dem Zusammenhang
\frac{F}{\dot{m}_{\mathrm e}}=v_{\mathrm e}, der aus der oben angegebenen Formel für die Schubkraft folgt.
Einsetzen der Integrationsgrenzen 0 und t ergibt:
\begin{aligned}
v &= -v_{\mathrm e} * \left( \left[ \ln{(m_0-\dot{m}_{\mathrm e}*t)} \right] - \left[ \ln{(m_0)} \right] \right) \\
&= -v_{\mathrm e} * \ln \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) \\
\end{aligned}
Diesen Ausdruck kann man nun in die Formel für die kinetische Energie der Rakete einsetzen:
E_{kin}=\frac{1}{2} * m * v^2 = \frac{1}{2} * (m_0-\dot{m}_{\mathrm e}*t) * v_{\mathrm e}^2 * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)
Leider kann man dieser Formel nicht unmittelbar ansehen, ob sie stärker oder weniger stark als linear ansteigt, sicher ist jedoch, dass sie nicht linear ansteigt. Das scheint nicht mit einem linearen Verbrauch an Antriebsenergie zusammenzupassen. Dafür gibt es jedoch eine einfache Erklärung. Die Antriebsenergie wird nicht nur in kinetische Energie der Rakete umgewandelt, sondern auch in kinetische Energie der ausgestossenen Rückstossmasse. Erst die Summe aus diesen beiden kinetischen Energien entspricht der Antriebsenergie. Es muss also auch die kinetische Energie der ausgestossenen Rückstossmasse berechnet werden.
Betrachtet man einen extrem kleinen Teil der Rückstossmasse, so ergibt sich für dessen kinetische Energie relativ zum Ruhesystem (in dem die Rakete zum Zeitpunkt t = 0 ruht) :
dE_{ekin}=\frac{1}{2} * dm * (v-v_e)^2
Die Geschwindigkeit der Rückstossmasse relativ zum Ruhesystem entspricht dabei der Geschwindigkeit der Rakete relativ zum Ruhesystem minus der Ausstossgeschwindigkeit der Rückstossmasse relativ zur Rakete.
Um die Summe der kinetischen Energie der gesamten ausgestossenen Rückstossmasse zu ermitteln, muss diese Gleichung über die Zeit integriert werden. Die Rückstossmasse dm wird dabei entsprechend dem Zusammenhang
dm=\dot{m}_{\mathrm e}*dt durch die in einem extrem kleinen Zeitraum dt ausgestossene Rückstossmasse ersetzt, und die Geschwindigkeit v der Rakete durch den weiter oben ermittelten Ausdruck.
\begin{aligned}
E_{ekin} &= \int_0^t \frac{1}{2}*\dot{m}_{\mathrm e}*(v-v_e)^2\,dt \\
&= \frac{1}{2} * \dot{m}_{\mathrm e} * \int_0^t (v-v_e)^2\,dt \\
&= \frac{1}{2} * \dot{m}_{\mathrm e} * \int_0^t \left( -v_{\mathrm e} * \ln \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)-v_e \right)^2\,dt \\
&= \frac{1}{2} * \dot{m}_{\mathrm e} * \int_0^t \left( -v_{\mathrm e} * \left( \ln \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)+1 \right) \right)^2\,dt \\
&= \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * \int_0^t \left( \ln \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)+1 \right)^2\,dt \\
\end{aligned}
Das Integral ist nicht allzu schwierig manuell zu lösen, mir fehlt jedoch die Zeit, um auf die Zwischenschritte einzugehen. Deshalb sei die Lösung hier Wolfram Alpha überlassen. Aufgrund der Einschränkungen von Wolfram Alpha bei Variablennamen verwende ich dabei q für
\dot{m}_{\mathrm e}.
∫ (ln(1-q*t/m_0)+1)^2 dt
Dieser Ausdruck kann nun (leicht zusammengefasst) in die obige Gleichung für die kinetische Energie der ausgestossenen Rückstossmasse eingesetzt werden. Das Einsetzen der Integrationsgrenzen verändert den Ausdruck nicht, da sich für t = 0 Null ergibt.
\begin{aligned}
E_{ekin} &= \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * \left[ \left( t-\frac{m_0}{\dot{m}_{\mathrm e}} \right) * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)+t \right]_0^t \\
&= \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * \left( \left( t-\frac{m_0}{\dot{m}_{\mathrm e}} \right) * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)+t \right) \\
\end{aligned}
Sofern alles stimmt, sollte nun die Summe der kinetischen Energie der Rakete und der kinetischen Energie der Rückstossmasse einen linearen Ausdruck für die Antriebsenergie ergeben:
\begin{aligned}
E_{prop} &= E_{kin}+E_{ekin} \\
&= \frac{1}{2} * (m_0-\dot{m}_{\mathrm e}*t) * v_{\mathrm e}^2 * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) \\
&\hphantom{\,=\,} + \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * \left( \left( t-\frac{m_0}{\dot{m}_{\mathrm e}} \right) * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right)+t \right) \\
&= \frac{1}{2} * (m_0-\dot{m}_{\mathrm e}*t) * v_{\mathrm e}^2 * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) \\
&\hphantom{\,=\,} + \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * \left( t-\frac{m_0}{\dot{m}_{\mathrm e}} \right) * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) + \frac{1}{2}*\dot{m}_{\mathrm e} * v_{\mathrm e}^2 * t \\
&= \cancel{ \frac{1}{2} * (m_0-\dot{m}_{\mathrm e}*t) * v_{\mathrm e}^2 * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) } \\
&\hphantom{\,=\,} + \cancel{ \frac{1}{2} * (\dot{m}_{\mathrm e}*t-m_0) * v_{\mathrm e}^2 * \ln^2 \left( 1-\frac{\dot{m}_{\mathrm e}*t}{m_0} \right) } + \frac{1}{2} * \dot{m}_{\mathrm e} * v_{\mathrm e}^2 * t \\
&= \frac{1}{2}*\dot{m}_{\mathrm e} * t * v_{\mathrm e}^2 \\
\end{aligned}
Bemerkenswerterweise heben sich grosse Teile des Ausdrucks gegeneinander auf, und übrig bleibt eine einfache lineare Formel, die tatsächlich der Antriebsenergie entspricht. Die Antriebsenergie ist unabhängig von der Geschwindigkeit der Rakete, und entspricht (idealisiert -- d.h. ohne Berücksichtigung von Verlusten) der Energie, die notwendig ist, um die Rückstossmasse auf die Ausstossgeschwindigkeit v
e relativ zur Rakete zu beschleunigen.
Zur Veranschaulichung nun noch ein konkretes Beispiel: Eine Rakete mit einer Anfangsmasse von 1000 kg (inkl. Treibstoff) stosse 10 kg Rückstossmasse pro Sekunde mit einer Geschwindigkeit von 2000 m/s aus. Während des Flugs wirken keine relevanten externen Kräfte (z.B. Gravitation) auf die Rakete. Das entspricht den folgenden Werten:
| \text{Bezeichner} | \text{Wert} | | m_0 | 1000\,\mathrm{kg} |
| \dot{m}_{\mathrm e} | 10\,\mathrm{kg/s} |
| v_{\mathrm e} | 2000\,\mathrm{m/s} |
| F | 20.000\,\mathrm{N} |
Die folgende Grafik zeigt den Verlauf der verbrauchten Antriebsenergie, der kinetischen Energie der Rakete und der kinetischen Energie der ausgestossenen Rückstossmasse:
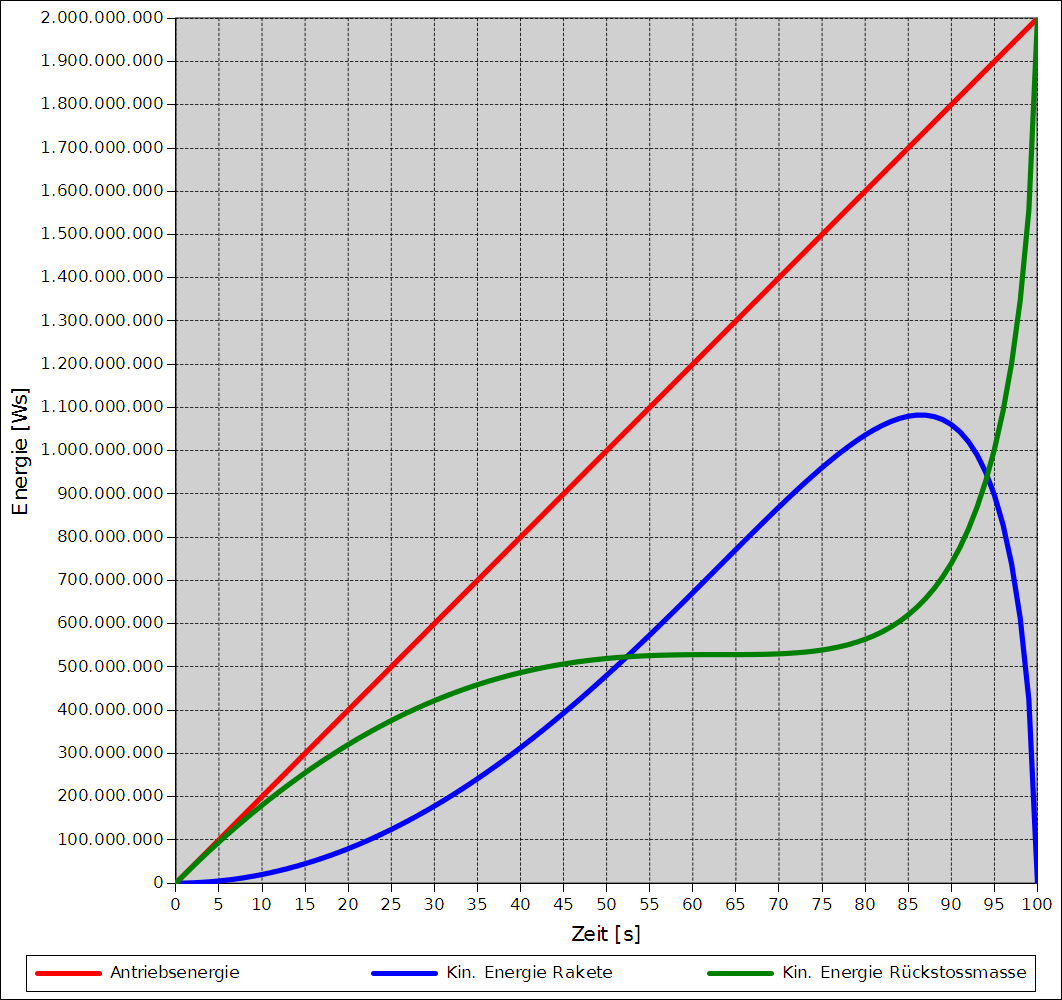
Die Grafik zeigt, dass die kinetische Energie der Rakete (blaue Kurve) stets deutlich unter der verbrauchten Antriebsenergie (rote Kurve) bleibt. Bei einer realen Rakete würden die Kurven natürlich deutlich früher enden (bzw. in einen konstanten Verlauf übergehen), da eine reale Rakete nicht zu 100% aus Rückstossmasse besteht.
Die Grafik habe ich mit der Linux-Tabellenkalkulation Gnumeric erstellt. Falls sich jemand näher damit beschäftigen möchte (die Grafik passt sich automatisch an die eingegebenen Werte für
m_0,
\dot{m}_{\mathrm e} und
v_{\mathrm e} an), hier die Gnumeric-Datei zum Download:
Dateianhang: Raketen_Energieerhaltung.gnumeric (5 KB)Der Zeitpunkt des Maximums der kinetischen Energie der Rakete lässt sich mit der folgenden Formel berechnen (aus Zeitgründen ohne Herleitung):
t = \left( 1-\frac{1}{e^2} \right) * \frac{m_0}{\dot{m}_{\mathrm e}} ≈ 0{,}865 * \frac{m_0}{\dot{m}_{\mathrm e}}
Moral von der Geschicht: Man darf in der Physik alles in Frage stellen, aber die Erfahrung zeigt, dass die Erhaltungssätze stets das Letzte sind, das man in Frage stellen sollte.
;)uatu schrieb:Deine erste Frage ist etwas aufwändiger zu beantworten, aber kurz zur zweiten:











