Dekohärenz und der Zufall in der Quantenmechanik

Zu der Frage "Gibt es Zufall in der Quantenmechanik?" aus diesem Thread: Quantenmechanik: Objektiver Zufall
--------------------------------------------------------------------------------------------------------------------------------
In diesem Zusammenhang sollte ich dir vielleicht den Begriff der Dekohärenz ans Herz legen. Die Quantenmechanik und ihre Formeln enthalten grundsätzlich erst mal keine Zufälle, man sagt dass die QM deterministisch ist (wenn man eine Determinismusdefinition benutzt, die sich nicht mit der Lichtgeschwindigkeit beißt). Das bedeutet: Jeder Zustand eines Systems definiert den exakten nächsten Zustand im nächsten kleinen Zeitschritt. Da ist kein Zufall dabei, alles ist sauber definiert.

Lass mich ein kleines Beispiel anbringen:

Wir betrachten mal folgende physikalische Theorie:

A->B->C->D->A

So solle sich das physikalische System verhalten. Wenn es sich im Zustand A befindet dann befindet es sich im nächsten Zeitschritt in B, im nächsten in C und so weiter und irgendwann wieder in A. Und dann von vorne.

Diese Theorie ist deterministisch. Wenn ich den aktuellen Zustand kenne weiß ich genau, wie es in 1000 Zeitschritten aussieht. Und insbesondere bedeutet das, dass wenn ich die Zeit erst laufen lasse und dann um das gleiche Intervall rückwärts laufen lasse (wie immer ich das praktisch auch anstellen mag) dann komme ich wieder bei meinem Ausgangspunkt an.

Jetzt führen wir mal einen Zufall ein: Der Alte hat einen großen Würfel. Der Würfel hat 1000 Seiten er würfelt in jedem Zeitschritt. Jedes Mal wenn er ne 20 würfelt dann überspringt das System einen Zustand, und geht z.B. statt von A->B sofort A->C. Das ist Zufall. Und das führt dazu, dass die Theorie nicht mehr deterministisch ist: Wenn ich die Zeit rückwärts laufen lasse dann komme ich nicht zwangsläufig wieder am ursprünglichen Zustand an.

In der Quantenmechanik gibt es einen solchen Zufall NICHT!. In der Quantenmechanik gibt es einen streng deterministischen Zusammenhang zwischen den Zuständen.

Zustände schreibt man in der Quantenmechanik idr. so:
|A> |B> |C>
Aber das bedeutet in etwa das Gleiche wie wenn ich die Zustände einer Münze (Kopf und Zahl) betrachte:
|K> |Z>
Ist nur eine fancy Schreibweise.
Für diese Zustände gibt es jetzt feste Regeln wie sie ineinander übergehen, genau wie bei dem ABCD-System von oben. Mit dem kleinen Unterschied dass jetzt Zustände zueinander addiert werden dürfen (was bei einer Münze nicht so ganz ersichtlich wäre, was das bedeutet)
|K>+|Z> = |lol>

Weil diese Theorie deterministisch ist kann ich die Zeit auch rückwärts laufen lassen und ich müsste wieder zum Ausgangszustand zurück kommen, und genau das ist auch bei der Quantenmechanik der Fall.

Schieße ich ein Elektron durch einen Spalt dann wir das Elektron gebeugt. Die Richtung (der vertikale Impuls) des Elektrons verändert sich (scheinbar zufällig) und es fliegt irgendwo nach links oder nach rechts.
Wenn ich die Zeit jetzt rückwärts laufen lasse (und es gibt tatsächlich Versuchsanordnungen, die einen solchen praktischen Effekt auf das Elektron haben können) dann kommt das Elektron wieder exakt gerade aus dem Spalt heraus. Es wird NICHT ein Zweites mal gebeugt, es fliegt seinen exakten Pfad zurück bis zur Quelle und ist dort dann mit 100%er Sicherheit wieder anzutreffen.

Was ist dann also wirklich mit dem sog. Zufall in der Quantenmechanik? Was ist zufällig, und was ist deterministisch.

Nun, um es auf den Punkt zu bringen: Die Messung ist zufällig. Der Rest nicht. Gehen wir mal darauf ein, was eine Messung eigentlich macht:

Ich hab bereits erläutert dass es in der QM Zustände |A> gibt. Am besten stellt man sich diese Zustände als "Wolken" im Raum vor, die unterschiedlich dicht an verschiedenen Stellen ist.

Eine solche Wolke könnte z.B. so aussehen:



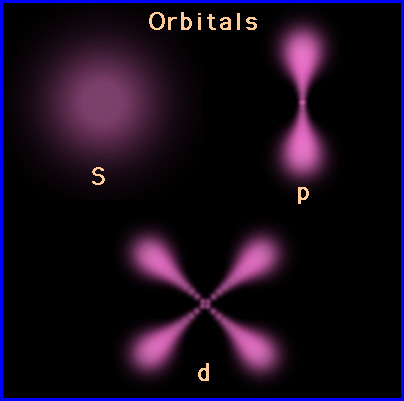
Allerdings ist die Wolke nicht nur reel sondern auch imaginär (also eine Wolke komplexer Zahlen), aber das soll uns hier nicht weiter beschäftigen.

Diese Wolke ändert sich ständig aufgrund der physikalischen Einflüsse die auf sie wirken. Beschrieben wird das durch die sogenannte Schrödingergleichung. Und weil das ganze oftmals wie eine wellenartige Bewegung zwischen den reellen und komplexen Anteilen aussieht nennt man die Wolke gern Wellenfunktion. Ein etwas unglücklicher Begriff, weil er sprachlich andere Dinge impliziert als er tatsächlich meint, aber nun gut damit muss man eben klar kommen.

Also, Zustände kann man sich als diese lustigen Wolken vorstellen. Und wie ich bereits gesagt habe könnten Zustände addiert werden und dann passiert auch in der Schrödingergleichung.
|A>+|B> = |neuer Zustand>
Zwei Zustände werden addiert und es kommt wieder ein sinnvoller Zustand raus.

Jeder Zustand lässt sich als die Summe von anderen Zuständen darstellen. Das ganze nennt sich Fourier-Theorie und ist etwas unhandlich wenn man nicht in der Mathe drinnen ist, aber so wie die Zahl 10 sowohl 1+9 als auch 2+8 ist, so kann man jede Wellenfunktion auch als die Summe von veschiedenen anderen Wellenfunktionen darstellen.

Das ist wie beim Schall: Du hörst mit deinem Ohr ganz viele verschiedene Sinuswellen mit unterschiedlichen Frequenzen, aber zusammen ergibt sich ein sehr komplexes Tonsignal, z.B. einen Song aus dem Radio.
Dieses Lied lässt sich als eine Summe von Sinus-Wellen mit verschiedenen Frequenzen darstellen. Aber das ist nicht die einzige Möglichkeit. Zum Beispiel könnte ich als "Grundbausteine" statt der Sinuswellen auch irgendwelche Rechteckimpulse benutzen und dann geschickt zusammensetzen.
Oder ich benutze Töne die aus einem sehr kurzen lauten "Knacken" an einem einzelnen Zeitpunkt bestehen: Eine Signal hat ein Knacken bei 1,1s , das nächste Signal bei 1,10000001 usw.
Wenn ich davon ganz viele nehme kann ich wieder mein Lied zusammensetzen durch die Summe der Grundbausteine.

Wellenfunktionen lassen sich ebenso in "Grundbausteine" oder "Eigenzustände" zerlegen. Und jeder Satz von Grundbausteinen gehört zu einer bestimmten Größe, die zu dem System gehört.

Z.b. hat ein Elektron eine Eigenschaft namens Position, und dementsprechend gibt es eine Reihe von Moden
|x1> |x2>... usw.
die zu dieser Eigenschaft gehören. Wenn ein System z.B. in dem Zustand |x1> ist, dann bedeutet das, dass das Teilchen exakt bei der Position 1 ist.
Eine andere physikalische Größe könnte der Impuls des Elektons sein, und damit einher gehen die dazugehörigen Zustände:
|p1> |p2> ...
Wenn ein Teilchen jetzt in dem Zustand |p1> ist, dann hat genau den Impuls 1.

Der Gag daran ist jetzt, dass die Eigenzustände für verschiedene Systemgrößen unterschiedlich sind. Es gibt kein |x> das mit einem |p> gleich ist.
Das bedeutet, wenn das System in dem Zustand |x14> ist, dann lässt sich die Wellenfunktion als die Summe von einem Positions-Eigenzustand darstellen, nämlich genau |x14>. Aber es gibt kein |p> das genau die richtige Form hat, deswegen muss ich, wenn ich die Bausteine vom Impuls benutzen will mehrere |p>s:

|x14> = 0,1* |p1> + 0,4 * |p2> + 100 * |p3> +...

Grundsätzlich gilt: Je weniger |x> Zustände ich brauche um mein System darszustellen, desdo mehr |p> Zustände brauche ich. Einfach weil die Eigenzustände (charakteristische Wolkenformen) der Position und des Impulses komplett verschieden aussehen.

So, jetzt wieder zur Messung. Eine Messung bestimmt eine bestimmte Größe, genauer gesagt, einen bestimmten Typ von Eigenzuständen. Ein Messgerät für Positionen kann zum Beispiel die Eigenzustände |x> bestimmen. Aber es misst immer nur einen bestimmten Eigenzustand.

Das Messgerät wird für das System 0.1*|x1> + 0.9*|x2> wird zum Beispiel mit 10% Wahrscheinlichkeit |x1> anzeigen und mit 90% Wahrscheinlichkeit |x2>. Es kann keine "gemischten" Zustände anzeigen, nur die Eigenzustände. Bei der Messung wird das System auch in den enstprechenden Eigenzustand versetzt. D.h.
das System, das vorher so aussah:

0.1*|x1> + 0.9*|x2>

sieht nach einer Positionsmessung nun so aus:

1.0*|x2>

Man hat das System also manipuliert.

Das bedeutet aber auch, dass die Summe der |p>s, die das System ebenfalls beschrieben haben nun komplett anders aussieht. Logisch, denn 0.1*|x1> + 0.9*|x2> hat eine andere |p>-Summe als |1.0*|x2>.

So und nach dem ganzen vielen Text sind wir jetzt endlich bei deinem Zufall angekommen: Wer entscheidet, welchen Eigenzustand das Messgerät anzeigt :) ? Ist das Zufall? Würfelt Gott?

Nein. Es gibt keinen Zufall in der QM. Nicht in dem Würfel-Sinne. Lass mich das Problem so angehen:

Habe ich ein einzelnes Teilchen im Zustand |A> dann weiß ich genau, wie es sich verhält. Ich braucht bloß mit der Schrödinger-Gleichung rumrechnen und weiß dann, AHA, nach 10s ist das Teilche in Zustand |F>.
Was passiert wenn ich ein zweites Teilchen (Zustand |B>) dazubringe und beide interagieren? Ganz einfach: Schrödingergleichung und rumrechnen.
Drittes Teilchen? Schrödingergleichung.
Viertes Teilchen? Schrödingergleichung.
Fünfmilliardstes Teilchen? Schrödingergleichung.
Mhh ach moment, langsam wird es schwierig zu rechnen. Aber das ändert ja nix an der Gleichung oder? Sollte doch
theoretisch
alles berechenbar sein, oder?
Richtig, ist es auch. Unter der Voraussetzung, dass ich die exakten Zustände der Teilchen auch kenne.

Kenne ich den exakten Zustand der Teilchen nicht muss ich statistisch Rechnen. Glücklicherweise verhalten sich große Quantenmechanische System nach sehr schönen Verteilungsfunktionen, die allesamt recht intuitiv erfassbar sind (nennt sich klassische Mechanik). Die Quantenmechanik gebietet nun durch ihre Regeln, dass sie einzelne Teilchen bei Kontakt mit einem riesigen System sehr schnell "darin verlieren" oder "eingliedern". Oder mit anderen Worten: Kommt ein Teilchen in Kontakt (d.h. es wechselwirkt stark) mit einem sehr komplexen System, dann wird die kleine Wellenfunktion des armen Teilchens einmal richtig ordentlich durchgeschüttelt, und am Ende sieht es komplett anders und vor allem sehr klassisch aus.

Schnappen wir uns also mal ein Elektron in dem Zustand |x1> + |x2> und bringen es in Kontakt mit einem RIESIGEN Quantensystem. Dieses Quantensystem ist genau so gestaltet, dass es Energiesenken hat, in die wunderbar ein |x1>-Elektron oder ein |x2>-Elektron passen würde. Das ganze oszilliert ein bisschen, also kommt es auf den genauen Zeitpunkt an.

Sagen wir mal, die Senke passt gerade an ein |x1>-Elektron: Die Wellenfunktion des Elektrons wechselwirkt jetzt mit dem großen Objekt, wabbert ein bisschen herum und bleibt dann letztendlich schön sauber in dem Senke liegen, wie ein Ball in einem Tal. Vielleicht passt die Senke nicht besonders gut, dann wackelt es sehr lange, bis es sich einpasst. Vielleicht passt die Senke aber auch sehr, sehr gut, dann wackelt es nicht so lange. In jedem Fall kommt es irgendwann in der Senke zum liegen. Das ist Dekohärenz: Der |x2>-Anteil des Elektrons verschwindet, weil er an dem riesigen System abfedert wie ein Hammer an einer Gummiwand und irgendwann seine Energie komplett verloren hat.

Das gleiche Prinzip gilt natürlich auch für die |x2>-Senke.

Was passiert jetzt aber, wenn das große System furchtbar schnell oszilliert. Und schlimmer noch: Ich kenne den Zustand des Systems nicht? Mal ist es eine |x1>-Senke, mal eine |x2>-Senke? Mal so mal so. Dann haben wir ein Problem. Das große System (ich nenne es jetzt einfach mal Messgerät) ist nur noch statistisch erfassbar. Ich weiß grob was es macht: |x>-Senken erzeugen. Aber weil ich den Zustand nicht kenne, und es aufgrund seiner immense Größe so schnell oszilliert weiß ich nie genau, welche Senke gerade vorhanden ist. Wenn ich jetzt mein Elektron an das Messgerät heranbringe ist es im Prinzip totaler Zufall was passiert. Eventuell fällt es in die eine Senke, villeicht aber auch in eine andere Senke. Vielleicht wechselt die Wellenfunktion des Messgeräts aber auch so schnell, dass es während es schon fast in einer Senke drin war plötzlich in eine andere Senke fällt? Absolut zufällig, was passiert. Aber nicht weil das Elektron zufällig ist. Nicht weil die Quantenmechanik zufällig ist. Das einzige was zufällig ist, ist mein Wissen über das Messgerät. Solange ich nicht weiß, wie das Messgerät aufgebaut ist und welchen exakten Zustand es hat kann ich nicht sagen was passiert. Wüsste ich den Zustand des Messgeräts könnte ich dir exakt vorherberechnen (Rechenpower vorausgesetzt) was passiert, genau wie bei jeder anderen Teilchen-Teilchen-Interaktion. So aber muss man sich damit zufrieden geben zu sagen, welche |x>-Zustände wahrscheinlicher die Dekohärenz an diesem riesen Kuddel-Muddel-messgeräte-System überleben (weil sie von Beginn an stärker ausgeprägt waren und mehr Energie hatten) und somit "gemessen" werden. Aber Zufall ist da keiner dabei. Nur Unwissen. Und ich hoffe dass du auch den Unterschied zu einer Hidden-Variable-Theory weiter oben verstanden, denn das ist was ganz anderes als die Unwissenheit, die bei einem statistisch betrachteten Quantensystem auftritt.
--------------------------------------------------------------------------------------------------------------------------
Das ganze im Orginal gepostet hier:
Quantenmechanik: Objektiver Zufall (Seite 3) (Beitrag von HYPATIA)

Eins von dem, was ich noch nicht verstanden habe (inzwischen glaube ich, dass ich es eventuell nie verstehen werde):

Zustände in der QT sind doch Wahrscheinlichkeitsverteilungen? Das heißt aber immer, dass nur nach vielen Experimenten mit (idealerweise) identisch präparierten Systemen (was schon mit vielen Fragezeichen zu versehen wäre) Ergebnisse mit Aussagewert zu erwarten sind. Ich ziehe mich abermals an Großrechner Wilson/Mainz hoch: Der muss unzählige Male gleiche bzw. vergleichbare Rechenprozesse durchlaufen damit ein aussagekräftiges Ergebnis dabei heraus-kommt.

Das hat doch zunächst noch nichts mit Dekohärenz zu tun!?

Ich habe mir jetzt darüber zig Mal den Kopf zerbrochen, um nicht zu vorschnell eine dann schließlich doch wieder dumme oder naive Frage zu stellen:

Wie spannst du kausal einen Bogen von einem Ereignis in der Gegenwart (das als Einzel-Ereignis keinen Aussagewert hergibt) zu einem Universum, das in deinen Augen auf eine Weise deterministisch ist, dass bei einem zweiten Durchlauf wieder das Gleiche herauskäme? Ich zitiere dich:

Denn die QM an sich ist absolut streng deterministisch, ein System entwickelt sich aus den selben Grundbedingungen immer gleich weiter. Denn in der Schrödingergleichung gibt es für Zufälle keinen Platz, höchstens für Chaos, aber auch das ist und bleibt deterministisch.
Wenn ich das Universum von außen betrachten würde, also den gesamten Inhalt kennen würde (was den Begriff des Universums schon ad absurdum führt), und jetzt quantenmechanisch die Entwicklung des Universums untersuche, dann wird es sich immer gleich entwickeln. Ich kann es auch in Gedanken zurückspulen und es würde wieder das selbe machen.

Das ist doch eine bereits ewig währende Diskussion: Das kann schon sein! Das mag sein! Ich selbst bin auch viel mehr zum Determinismus geneigt als zu einem Glauben an seltsame Zufälle. Aber es geht doch um etwas anderes - vor allen Dingen doch immer wieder gerade dir selbst!:
Wir können das eben nicht nachvollziehen!

Dein Gedankenexperiment macht also keinen Sinn. Wenn ich jetzt im Hier und Heute schon nicht in der Lage bin zu sagen, was bei einem Versuch heraus-kommt und ein QT-Zustand eben nur einen Sinn ergibt, wenn er im Zusammenhang mit einer Vielzahl von durchgeführten Experimenten gesehen wird - wenn ich also im Hier und Heute nach EINEM Zeitschritt eben NICHT wissen kann, was heraus-kommt und das Ergebnis eben stets nur seine Aussagekraft erhält im Zusammenhang mit dem Gesetz der großen Zahlen:

Wie um alles in der Welt soll es dann nachvollziehbar sein, dass sich das gesamte Universum (würde man die Zeit zurück-drehen) bei einem zweiten Durchlauf sich wieder genau so entwickeln soll?

Wo liegt denn da der Kern der (oder nur meiner?) Verwirrung?

Lieber Gruß

sunaJJanus schrieb:Zustände in der QT sind doch Wahrscheinlichkeitsverteilungen?

Nein, Zustände schon überhaupt nicht. Wenn du den Betrag der Wellenfunktion quadrierst und dann normierst dann erhälst du die Wahrscheinlichkeitsdichte darüber, welcher Zustand nach einem Dekohärenzvorgang dominiert (das lässt sich mathematisch zeigen).

Der Zustand selbst ist die Information, die in dem System steckt, und sie ist auch die gesamte Information. Mehr gibt es nicht. Insbesondere ist der "Ort" eines Teilchens, den du misst keine Information. Durch die Messung veränderst du das System.

In der Anfangszeit der QM hat man zunächst empirisch festgestellt, dass eben das Betragsquadrat der Wellenfunktion als Wahrscheinlichkeitsdichte für Messungen benutzt werden kann, deshalb hat man in der "Kopenhagener Interpretation" eben das Experiment mithilfe dieser Verwendung der Wellenfunktion an die Theorie gekoppelt.

Die QM steckte da aber noch in den Kinderschuhen, man war genug damit beschäftigt auf dieser Basis zu arbeiten. Später hat man dann eben den Bogen weiter gespannt und auch Überlegungen dazu angestellt, wie das Messgerät als Quantenmechanisches Objekt betrachtet werden kann. Denn schließlich muss die QM, wenn sie denn eine gültige physikalische Theorie sein soll und im Rahmen des Korrespondenzprinzips auch die klassische Mechanik enthalten soll, auch ein Messgerät sinnvoll beschreiben können. Darüber kommt man dann zur Dekohärenz.

sunaJJanus schrieb:Das heißt aber immer, dass nur nach vielen Experimenten mit (idealerweise) identisch präparierten Systemen (was schon mit vielen Fragezeichen zu versehen wäre) Ergebnisse mit Aussagewert zu erwarten sind.

Wie gesagt, wir müssen uns darauf einigen, dass auch das Messgerät ein Quantenobjekt ist. Sonst macht die Diskussion überhaupt keinen Sinn. Wenn das Messgerät kein Quantenobjekt ist dann können wir es mit Quantenmechanik nicht beschreiben. Dann braucht man eben eine Erweiterung der Theorie, die die beiden Welten miteinander verknüpft (was eben der Zufall der Kopenhagener Interpretation wäre).
Ist das Messgerät aber ein Quantemechanisches Objekt, dann verhält es sich auch nach den Quantenmechanischen Gesetzen.
Und da kann ich dir dann ganz klar sagen, wenn das System (Untersuchter Gegenstand+Messgerät) zweimal im gleichen Zustand ist, dann kommt auch genau das gleiche raus.
In der Praxis kannst du aber das Messgerät nicht präparieren, weswegen das System eben NICHT wieder im gleichen Zustand ist, ergo erhälst du ein anderes Messergebnis.

Eine reine Wahrscheinlichkeitsinterpretation der Wellenfunktion ist auch etwas naiv, weil sie eben viel mehr leistet als nur das. Im Doppelspaltversuch geht das Teilchen durch BEIDE spalte, und wechselwirkt mit sich selber.
Oder um bei einem anschaulichen Beispiel zu bleiben:
Schrödingers Weinbergschnecke (Katzen sind leider keine Hermaphroditen) kann in der Kiste schwanger werden, weil viele Schnecken gleichzeitig existieren und miteinander agieren können. Quantemechanik dreht sich nicht nur um Wahrscheinlichkeiten, sondern um so viel mehr. Die Kopenhagener Interpretation ist fast schon eine Beleidigung dafür.

sunaJJanus schrieb:Wir können das eben nicht nachvollziehen!

Wir landen wieder außerhalb der QM. Wie das "echte" Universum funktioniert weiß ich nicht. Ein bisschen so wie ein quantemechanisches Universum würde ich schätzen. Das jedenfalls ist deterministisch.

Also was ich dir eben in einer PN geschrieben habe, fasse ich hier mal so zusammen, um es etwas "auf-zu-heitern":
Du hast rechts eine Mädchen-Schule und links eine Jungen-Schule und du beschreibst die "Wolken" im Pausenhof, die durch die umherlaufenden Mädchen und Jungs gebildet werden. Wenn nun die Jungs Bälle rüberschmeißen zu den Mädchen:
Dann kann man aus größerer Entfernung und ohne Fernglas nicht entscheiden, wo die Bälle landen werden - die Angelegenheit bleibt eine "Wahrscheinlichkeits-Geschichte".
Geht man aber nah dran: Dann sieht man, dass es eben DOCH immer ein jeweils ganz bestimmtes Mädchen ist, das einen ganz bestimmten Ball fängt?
Könnte man also in der QM "ganz nah dran gehen" - will sagen, könnte man Experimente identisch präparieren: Dann erhielte man auch stets eindeutige Ergebnisse?

Ich poste hier mal meine PM mit der Antwort:


Das Problem ist, wir haben noch keine Allgemeine Theorie, die das ganze Universum beschreiben kann. Damit können wir auch keine Allgemeinen Aussagen treffen.

Das Problem, um das es sich beider Quantemechanik dreht ist letztlich ihre "Interpretation". Dabei dreht es sich aber nicht um den Formalismus oder die Mathematik oder sonstwas, sondern darum, dass wir Menschen letztlich nur "klassische" Informationen wahrnehmen.

Die Quantentheorie sollte ja an sich für alles gültig sein, was nicht zu hohe Massen und Geschwindigkeiten betrifft. Das bedeutet auch insbesondere, dass ein Mensch nur ein chemischer Baukasten sein sollte, der nach den Regeln der Quantenmechanik spielt.

Wenn ich nun große Systeme betrachte dann tritt eben ein Dekohärenzeffekte auf, d.h. der Zustand des Systems "pendelt" sich sehr schnell auf eine bestimmten Eigenzustand ein. Dieses Einpendeln ist für alle praktischen Belange als zufällig ansehbar, weil er zu komplex ist. Eine technische Beschreibung des Vorgang ist aber dennoch mit Quantenmechanischen Methoden möglich (zumindest theoretisch). Ich kann also exakt sagen, was ein Messgerät anzeigen wird, sofern ich den exakten Zustand des Messgeräts kennen würde (aus praktischen Gründen nicht machbar, theoretisch aber wäre das Messgerät präparierbar).

Die Sache ist jetzt die: Wenn ich eine solche hypothetische Rechnung durchführen würde, dann kommt eben NICHT ein Eigenzustand als Anzeige auf dem Messgerät heraus. Das Messgerät ist nach Quantenmechanischen Berechnungen immer noch in einer Superposition. Zwar gibt es einen einzelnen Eigenzustand, der das System MASSIV dominiert (genau den würde ich dann auch in der Realität beobachten können), aber die anderen Anteile sind laut Rechnung nicht komplett verschwunden, sondern werden nur winzig, winzig klein.

Die Frage ist nun, warum sehen wir nur den dominierenden Ausschlag am Messzeiger, haben aber keine Chance die Superposition am Messgerät zu beobachten?
Das ist das eigentliche Problem: Ich kann die Quantenmechanik immer weiter "nach oben" weiterziehen, immer größere Systeme betrachten. Damit wird aber nie das Paradoxon mit den überlagerten Zuständen ausgelöscht.

Schlimmer noch, je größer das System ist, das wir mit Quantenmechanik betrachten, desto nutzloser wird die Theorie. Dann treten Effekte auf, die mit ihr nicht mehr erklärbar sind und der Relativitätstheorie bedürfen.

Es gibt also eine massive Lücke irgendwo in unserem Wissen, ohne die wir nicht weiterkommen. Ich persönlich denke, und lehne mich dabei ganz weit aus dem Fenster, dass dieses Problem letztlich mit einer Erklärung des Phänomens "Bewusstsein" einhergeht, das wir zum jetzigen Zeitpunkt ebenfalls nicht verstehen können.

Das meinte ich eben in den entsprechenden Threads: Der Zufall ist nicht unser Problem, die Quantemechanik erklärt schon, warum EIN BESTIMMTER Zustand selektiert wird. Praktisch ist das zwar nicht von Bedeutung, aber die Mathematik der QM ist an dieser Stelle nicht "unvollständig". Viel größer ist das Problem, warum wir trotz vorhergesagter Superpositionen keine Beobachten können. Dass die Superpositionen ULTRASCHWACH sind, ist zwar schön und gut, aber irgendwie auch keine befriedigende Erklärung.

Schade, dass es nicht mehr solcher Blogs hier gibt.

Weiter so!