Superluminales Tunneln
14.09.2006 um 14:37hallo,
hier der versprochene thread. ich möchte den bekannten tunneleffekt maletwas genauer beschreiben und verdeutlichen, warum der verbreitet mythos der"überlichtgeschwindigkeit" nicht stimmt.
soviel dazu, zur ausführung:
zuerstmal die frage, was ist tunneln überhaupt??
die physikalischeerklärung dafür lautet wie folgt:
die quantenmechanik beschreibt es als vorgang,in der eine welle (oder ein wellenpaket) auf eine potentialbarriere trifft. dabei hat daswellenpaket weniger energie als es tatsächlich braucht, um diese barriere zu überwinden.
die sogen. "schrödingergleichung" -->
bietet gewisse lösungen, die sich auf diebereiche zwischen den wänden einer solchen barriere beziehen. dabei gilt es zubeachten, dass ein zerfall umso schneller von statten geht, je grösser derpotentialunterschied ist (also zwischen wellenenergie und barrierenhöhe).
hier mal bildlich dargestellt:
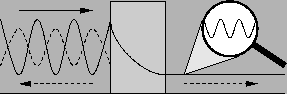
dabei trifft ein wellenpaket auf eine potentialbarriere. die enrgie reicht alsonicht aus und somit passiert folgendes: der eine teil der welle wird reflektiert, derandere teil der welle durchtunnelt die barriere und breitet sich auf der anderen seiteweiter aus. daraus folgt, dass die intensität der tunnelwelle exponentiell abnimmt mitder energiedifferenz zwischen welle und barriere und auch mit der tunnelstrecke.
wenn die barriere einen "endlichen" wert hat (auf die breite bezogen), zerfälltdie welle nicht vollständig und somit kommt das "tunneln" überhaupt zu stande.
nun zur genaueren definition und erklärung:
es gibt zweibedeutende experimente, die gewichtung haben im superluminalen tunneln. zum einen das"nimtz-experiment" und zum andern das "chiao-experiment".
beide schneide ichhier mal kurz an.
das nimtz-experiment:
eingaußförmiges wellenpaket (frequenzbereich 8,2 - 9,2 GHz) wird durch eine tunnelstreckegeschickt, bestehend aus drei wellenleitern. die zwei äußeren wellenleiter (10.16 mm x22.86 mm) haben einen grenzfrequenzbereich von 6,56 GHz. somit also unter demfrequenzbereich, der hier beobachtet wird. der mittlere leiter jedoch hat maße von 7.90mm x 15.80 mm und somit einen grenzbereich von 9,49GHz. das impliziert, dass die wellendiese strecke also durchtunneln "müssen". wird jetzt die pulsform des wellenpaketsgemessen und mit einer referenzpulsform verglichen (auf einem anderen detektornatürlich), kann man folgendes feststellen:
1. ds wellenpaket wurde starkabgeschwächt (hohlleiter von längstesn 100mm, verhältnis 1500:1 für die Signalamplitudenvon Referenzkanal und Tunnelstrecke)
und
2. trifft das maximum desgetunnelten pulses nach 130 ps am detektor ein, das des referenzpulses jedoch erst nach200 ps.
die zuständigen des experiments haben damals den schluss daraus gezogen,dass sich das signal somit mit überlichtgeschwindigkeit ausgebreitet hat.
hier bildlich dargestellt:
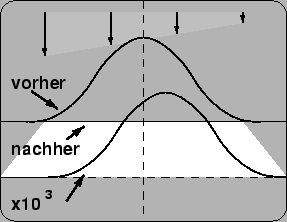
wenn eine barriere, wie hier, den hinteren teil des wellenpakets stärker dämpft, alsden vorderen, dann scheint das pulsmaximum nach vorne verschoben zu sein (hier erkenntman den ersten ansatz zur tatsächlichen erklärung).
daschiao-experiment ist im grunde dem nimtz-experiment gleich, mit der ausnahme, dassdas mikrowellenpaket nun ein einzelnes photon ist und die tunnelstrecke eine"zener-barriere" ist mit periodischer schichstruktur. auch bei deisem experiment wurdengeschwindigkeiten gemessen, die scheinbar über der lichtgeschwindigkeit lagen.
ok, jetzt zur erklärung des tatsächlichen vorgangs beim tunneln.
fragtman, was denn nun genau passiert beim tunneln, ann man das mit einem zitat leichtbeantworten:
das Signal verformt sich während des Tunnelns.
washeisst das genau?
also....
es gibt eine veröffentlichung diversercomputerprogramme, die physikalische probleme numerische behandeln. eines dieserprogramme löst die schrödingergleichung (zeitabhängig) in einer dimension und ausgehendvon einem völlig beliebigen, komplexen anfangszustand.
hier auch wiederbildlich dargestellt als numerische simulation:
1. t = 0,25
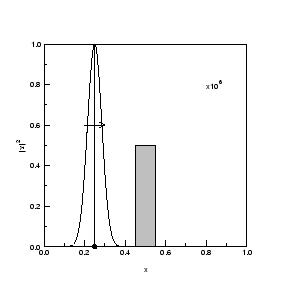
das signal nähert sich hier derpotentialbarriere.
das wellenpaket bewegt sich mit v=1. abgebildet ist hier
. die breite beträgt 
. die breite und der mittlere impuls sind sogewählt worden, das zu dem zeitpunkt (t=0,25) die amplitude des pakets imbarrierenbereich noch verschwindet. das intervall [0,1] wurde in schritten der breite10^-4 diskretisiert, der zeitschritt betrug 5 x 10^-7, die barrierenhöhe 2,0 x 10^4.
2. t = 0,37
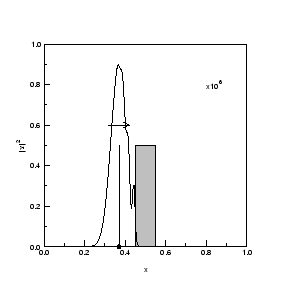
hier sind die auswirkungen der barriere auf das paket zu sehen.
erstewellenanteile werden reflektiert, in der nähe der barriere gibt esinterferenzerscheinungen. gruppengeschwindigkeit und paketmaximumsgeschw. sind zu demzeitpunkt noch definierte grösen.
3. [b]t = 0,45
zu sehen ist dieaufenthaltswahrscheinlichkeit bei t=0,45 , also zu dem Zeitpunkt, an dem ein klassischesTeilchen, welches sich ursprünglich am Paketmaximum befand und welches sich mit v=1bewegte, auf die Barriere trifft. Die interferenzbedingte Verformung des Wellenpakets istjetzt sehr stark.
die geschwindigkeit des paketmaximums ist jetzt nichtmehr vernünftig definiert, die maximums in der nähe von t=0,45 verändern für einen klarenzeitraum ihre amplitude, die position bleibt gleich.
4. [b]t =0,55
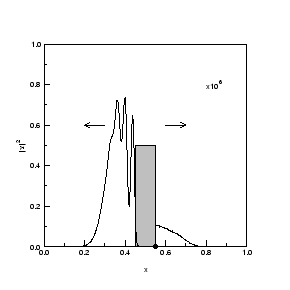
die reflektiondes pakets ist weit fortgeschritten, das tunnelsignal ist rechts schon zu erkennen.dassignal verformt sich dort schon und hat nicht mehr die urspüngliche gaußscheintensitätsverteilung.
5. [b]t = 0,65
das wellenpaket, dass reflektiert wurdeist fast wieder am ausgangspunt angekommen (x=0,25). der getunnelte teil rechts hat fastdas gaußsche intensitätsprofil, weist aber eine deutliche verformung auf.
das maximum einer gaußfunktion, die an das getunnelte Paket angepaßt wurde, befindetsich bei x=0,678. ohne die potentialbarriere wäre das maximum des wellenpakets nun beix=0,65. wenn die geschwindigkeit des pakets außerhalb der barriere konstant v=1 ist, somuß zu dem zeitpunkt, an dem das maximum des tunnelpakets das ende der tunnelstreckeerreicht, das nichttunnelnde paket erst bei x=0,522 gewesen sein. damit muß dasverhältnis der geschwindigkeiten der beiden pakete zwischen x=0,45 und x=0,55 gleich (0,55 - 0,45) / (0,522 - 0,45) = 1,389 gewesen sein.
es scheint, als hätte sichdas paket mit einer geschwindigkeit von v=1,389 ausgebreitet.
nunsind folgende sachen zu beachten, um das ganze zu einem abschluss zu bringen:
1. der betrag des getunnelten signals ist zu jedem zeitpunkt kleiner als der einesnichtgetunnelten signals wäre. es gibt auch kein intensitätsniveau, dass vom tunnelsignalfrüher erreicht wird als vom nichtgetunnelten signal.
2. die aufintegrierteintensität des getunnelten signals ist zu jedem zeotpunkt immer kleiner als die desnichtgetunnelten signals.
aus diesen beiden erkenntnissen folgt nun ein schluss:ein detektor eines bestimmten typs (hier nicht näher definiert, aber für ein experimentvon grosser bedeutung!!) registriert das nichttunnelnde signal in jedem fall früher alsdas getunnelte (unabhängig der detektorenempfindlichkeit). da nun das nichtgetunneltesignal höchstens mit c übertragen wurde, dann muss die geschwindigkeit derinformationsübertragung im tunnel für diese detektoren in jedem fall unter "c" liegen.
man stellt nun fest, dass das maximum des getunnelten signals gegenüber demdes nichtgetunnelten signals "nach vorne verschoben" ist. aus diesem grund folgern vieleauch, dass hier sowas wie "überlichtgeschwindigkeit" stattgefunden hat!!
die begründet sich auch recht einfach durch folgende zwei punkte:
1.der sender auf der linken tunnelseite hat eine endliche ansprechzeit. das heisst genau:vom zeitpunkt der sendeauslösung bis zum zeitpunkt, an dem der sender das signalmaximumemittiert, vergeht eine endliche zeit. wenn also der empfänger einen detektor benutzt,der das maximum detektiert, ist das nicht getunnelte signal auf jeden fall mitunterlichtgeschwindigkeit unterwegs. das getunnelte signal ist bei gleichem detektor dannschneller als das nicht getunnelte, aber die schlußfolgerung, daß das getunnelte signaldamit auch schneller als das licht sei, ist durch nichts gerechtfertigt.
2. wie erwähnt, ist der betrag des getunnelten signals jederzeit kleiner als der desnicht getunnelten signals (welches ja höchstens mit lichtgeschwindigkeit unterwegs ist).das heißt, daß das maximum des getunnelten signals beim empfänger erst eintreffen wird,nachdem das nicht getunnelte signal eine intensität erreicht hat, die dem maximum desgetunnelten signals entspricht. mithin wird ein detektor eines bestimmten typs, der aufgerade diese intensität eingestellt ist und das nicht getunnelte signal detektiert, dassignal früher registrieren als ein detektor, der das maximum des tunnelsignalsdetektiert. für diesen detektor aber war das nicht getunnelte signal höchstens mitlichtgeschwindigkeit unterwegs. da der detektor, der das maximum des tunnelsignalsdetektiert, erst später anspricht, muß das getunnelte signal mitunterlichtgeschwindigkeit übertragen worden sein.
soweitdie erklärung zum subluminalen tunneln.
letzte anmerkung:
ich habe ein etwas älteres skript gefunden, dass ich von einem meiner tutorenbekommen habe. daraus habe ich grösstenteils die textpassagen übernommen und nur leichtgeändert bzw. zusammengefasst. das skript beschreibt das tunneln recht verständlich,somit habe ich auf eigene formulierungen grösstenteils verzichtet. im internet müsstesich sicherlich auch eine quelle finden lassen, die als basis für das skript diente (sohats mir der tutor zumindest versichert). von dort sind auch die grafiken, die ich aufmeinem rechner habe und hier verwende. diese habe ich damals auch per email von meinemtutor erhalten.
also bitte keine beschwerden, dass dies nicht von mir stammt.;)
ich hoffe, das thema damit etwas genauer durchleuchtet zu haben.
R.[/b][/b][/b]
hier der versprochene thread. ich möchte den bekannten tunneleffekt maletwas genauer beschreiben und verdeutlichen, warum der verbreitet mythos der"überlichtgeschwindigkeit" nicht stimmt.
soviel dazu, zur ausführung:
zuerstmal die frage, was ist tunneln überhaupt??
die physikalischeerklärung dafür lautet wie folgt:
die quantenmechanik beschreibt es als vorgang,in der eine welle (oder ein wellenpaket) auf eine potentialbarriere trifft. dabei hat daswellenpaket weniger energie als es tatsächlich braucht, um diese barriere zu überwinden.
die sogen. "schrödingergleichung" -->
bietet gewisse lösungen, die sich auf diebereiche zwischen den wänden einer solchen barriere beziehen. dabei gilt es zubeachten, dass ein zerfall umso schneller von statten geht, je grösser derpotentialunterschied ist (also zwischen wellenenergie und barrierenhöhe).hier mal bildlich dargestellt:
dabei trifft ein wellenpaket auf eine potentialbarriere. die enrgie reicht alsonicht aus und somit passiert folgendes: der eine teil der welle wird reflektiert, derandere teil der welle durchtunnelt die barriere und breitet sich auf der anderen seiteweiter aus. daraus folgt, dass die intensität der tunnelwelle exponentiell abnimmt mitder energiedifferenz zwischen welle und barriere und auch mit der tunnelstrecke.
wenn die barriere einen "endlichen" wert hat (auf die breite bezogen), zerfälltdie welle nicht vollständig und somit kommt das "tunneln" überhaupt zu stande.
nun zur genaueren definition und erklärung:
es gibt zweibedeutende experimente, die gewichtung haben im superluminalen tunneln. zum einen das"nimtz-experiment" und zum andern das "chiao-experiment".
beide schneide ichhier mal kurz an.
das nimtz-experiment:
eingaußförmiges wellenpaket (frequenzbereich 8,2 - 9,2 GHz) wird durch eine tunnelstreckegeschickt, bestehend aus drei wellenleitern. die zwei äußeren wellenleiter (10.16 mm x22.86 mm) haben einen grenzfrequenzbereich von 6,56 GHz. somit also unter demfrequenzbereich, der hier beobachtet wird. der mittlere leiter jedoch hat maße von 7.90mm x 15.80 mm und somit einen grenzbereich von 9,49GHz. das impliziert, dass die wellendiese strecke also durchtunneln "müssen". wird jetzt die pulsform des wellenpaketsgemessen und mit einer referenzpulsform verglichen (auf einem anderen detektornatürlich), kann man folgendes feststellen:
1. ds wellenpaket wurde starkabgeschwächt (hohlleiter von längstesn 100mm, verhältnis 1500:1 für die Signalamplitudenvon Referenzkanal und Tunnelstrecke)
und
2. trifft das maximum desgetunnelten pulses nach 130 ps am detektor ein, das des referenzpulses jedoch erst nach200 ps.
die zuständigen des experiments haben damals den schluss daraus gezogen,dass sich das signal somit mit überlichtgeschwindigkeit ausgebreitet hat.
hier bildlich dargestellt:
wenn eine barriere, wie hier, den hinteren teil des wellenpakets stärker dämpft, alsden vorderen, dann scheint das pulsmaximum nach vorne verschoben zu sein (hier erkenntman den ersten ansatz zur tatsächlichen erklärung).
daschiao-experiment ist im grunde dem nimtz-experiment gleich, mit der ausnahme, dassdas mikrowellenpaket nun ein einzelnes photon ist und die tunnelstrecke eine"zener-barriere" ist mit periodischer schichstruktur. auch bei deisem experiment wurdengeschwindigkeiten gemessen, die scheinbar über der lichtgeschwindigkeit lagen.
ok, jetzt zur erklärung des tatsächlichen vorgangs beim tunneln.
fragtman, was denn nun genau passiert beim tunneln, ann man das mit einem zitat leichtbeantworten:
das Signal verformt sich während des Tunnelns.
washeisst das genau?
also....
es gibt eine veröffentlichung diversercomputerprogramme, die physikalische probleme numerische behandeln. eines dieserprogramme löst die schrödingergleichung (zeitabhängig) in einer dimension und ausgehendvon einem völlig beliebigen, komplexen anfangszustand.
hier auch wiederbildlich dargestellt als numerische simulation:
1. t = 0,25
das signal nähert sich hier derpotentialbarriere.
das wellenpaket bewegt sich mit v=1. abgebildet ist hier
. die breite beträgt . die breite und der mittlere impuls sind sogewählt worden, das zu dem zeitpunkt (t=0,25) die amplitude des pakets imbarrierenbereich noch verschwindet. das intervall [0,1] wurde in schritten der breite10^-4 diskretisiert, der zeitschritt betrug 5 x 10^-7, die barrierenhöhe 2,0 x 10^4.2. t = 0,37
hier sind die auswirkungen der barriere auf das paket zu sehen.
erstewellenanteile werden reflektiert, in der nähe der barriere gibt esinterferenzerscheinungen. gruppengeschwindigkeit und paketmaximumsgeschw. sind zu demzeitpunkt noch definierte grösen.
3. [b]t = 0,45
zu sehen ist dieaufenthaltswahrscheinlichkeit bei t=0,45 , also zu dem Zeitpunkt, an dem ein klassischesTeilchen, welches sich ursprünglich am Paketmaximum befand und welches sich mit v=1bewegte, auf die Barriere trifft. Die interferenzbedingte Verformung des Wellenpakets istjetzt sehr stark.
die geschwindigkeit des paketmaximums ist jetzt nichtmehr vernünftig definiert, die maximums in der nähe von t=0,45 verändern für einen klarenzeitraum ihre amplitude, die position bleibt gleich.
4. [b]t =0,55
die reflektiondes pakets ist weit fortgeschritten, das tunnelsignal ist rechts schon zu erkennen.dassignal verformt sich dort schon und hat nicht mehr die urspüngliche gaußscheintensitätsverteilung.
5. [b]t = 0,65
das wellenpaket, dass reflektiert wurdeist fast wieder am ausgangspunt angekommen (x=0,25). der getunnelte teil rechts hat fastdas gaußsche intensitätsprofil, weist aber eine deutliche verformung auf.
das maximum einer gaußfunktion, die an das getunnelte Paket angepaßt wurde, befindetsich bei x=0,678. ohne die potentialbarriere wäre das maximum des wellenpakets nun beix=0,65. wenn die geschwindigkeit des pakets außerhalb der barriere konstant v=1 ist, somuß zu dem zeitpunkt, an dem das maximum des tunnelpakets das ende der tunnelstreckeerreicht, das nichttunnelnde paket erst bei x=0,522 gewesen sein. damit muß dasverhältnis der geschwindigkeiten der beiden pakete zwischen x=0,45 und x=0,55 gleich (0,55 - 0,45) / (0,522 - 0,45) = 1,389 gewesen sein.
es scheint, als hätte sichdas paket mit einer geschwindigkeit von v=1,389 ausgebreitet.
nunsind folgende sachen zu beachten, um das ganze zu einem abschluss zu bringen:
1. der betrag des getunnelten signals ist zu jedem zeitpunkt kleiner als der einesnichtgetunnelten signals wäre. es gibt auch kein intensitätsniveau, dass vom tunnelsignalfrüher erreicht wird als vom nichtgetunnelten signal.
2. die aufintegrierteintensität des getunnelten signals ist zu jedem zeotpunkt immer kleiner als die desnichtgetunnelten signals.
aus diesen beiden erkenntnissen folgt nun ein schluss:ein detektor eines bestimmten typs (hier nicht näher definiert, aber für ein experimentvon grosser bedeutung!!) registriert das nichttunnelnde signal in jedem fall früher alsdas getunnelte (unabhängig der detektorenempfindlichkeit). da nun das nichtgetunneltesignal höchstens mit c übertragen wurde, dann muss die geschwindigkeit derinformationsübertragung im tunnel für diese detektoren in jedem fall unter "c" liegen.
man stellt nun fest, dass das maximum des getunnelten signals gegenüber demdes nichtgetunnelten signals "nach vorne verschoben" ist. aus diesem grund folgern vieleauch, dass hier sowas wie "überlichtgeschwindigkeit" stattgefunden hat!!
die begründet sich auch recht einfach durch folgende zwei punkte:
1.der sender auf der linken tunnelseite hat eine endliche ansprechzeit. das heisst genau:vom zeitpunkt der sendeauslösung bis zum zeitpunkt, an dem der sender das signalmaximumemittiert, vergeht eine endliche zeit. wenn also der empfänger einen detektor benutzt,der das maximum detektiert, ist das nicht getunnelte signal auf jeden fall mitunterlichtgeschwindigkeit unterwegs. das getunnelte signal ist bei gleichem detektor dannschneller als das nicht getunnelte, aber die schlußfolgerung, daß das getunnelte signaldamit auch schneller als das licht sei, ist durch nichts gerechtfertigt.
2. wie erwähnt, ist der betrag des getunnelten signals jederzeit kleiner als der desnicht getunnelten signals (welches ja höchstens mit lichtgeschwindigkeit unterwegs ist).das heißt, daß das maximum des getunnelten signals beim empfänger erst eintreffen wird,nachdem das nicht getunnelte signal eine intensität erreicht hat, die dem maximum desgetunnelten signals entspricht. mithin wird ein detektor eines bestimmten typs, der aufgerade diese intensität eingestellt ist und das nicht getunnelte signal detektiert, dassignal früher registrieren als ein detektor, der das maximum des tunnelsignalsdetektiert. für diesen detektor aber war das nicht getunnelte signal höchstens mitlichtgeschwindigkeit unterwegs. da der detektor, der das maximum des tunnelsignalsdetektiert, erst später anspricht, muß das getunnelte signal mitunterlichtgeschwindigkeit übertragen worden sein.
soweitdie erklärung zum subluminalen tunneln.
letzte anmerkung:
ich habe ein etwas älteres skript gefunden, dass ich von einem meiner tutorenbekommen habe. daraus habe ich grösstenteils die textpassagen übernommen und nur leichtgeändert bzw. zusammengefasst. das skript beschreibt das tunneln recht verständlich,somit habe ich auf eigene formulierungen grösstenteils verzichtet. im internet müsstesich sicherlich auch eine quelle finden lassen, die als basis für das skript diente (sohats mir der tutor zumindest versichert). von dort sind auch die grafiken, die ich aufmeinem rechner habe und hier verwende. diese habe ich damals auch per email von meinemtutor erhalten.
also bitte keine beschwerden, dass dies nicht von mir stammt.;)
ich hoffe, das thema damit etwas genauer durchleuchtet zu haben.
R.[/b][/b][/b]
