Frage zur Quantenmechanik
14.05.2021 um 18:50@Peter0167
Das sind interessante und schwierige Fragen. Ob du eine befriedignede Antwort bekommst ist unwahrscheinlich ;-)
Genauso ist auch der Ort nicht bestimmt. Man könnte flapsig sagen: Das Elektron ist gleichzeitig an verschiedenen Orten mit verschiedenen Geschwindigkeiten. Am besten ist es man verabschiedet sich von der Vorstellung von einem punktförmigen Etwas.
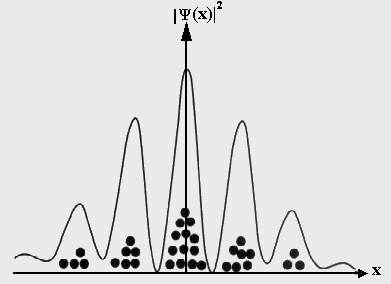
Stell dir dazu den Doppelspaltverusch vor mit einzelnen Elektronen. Bevor das Elektron an einem bestimmten Detektorpunkt aufkommt, ist es zuvor verschmiert an allen Orten gleichzeitig, allerdings mit verschiedenen Gewichtungen: An manchen Stellen ist das "Elektron" z.B. nur zu 20 % an andere zu 60 % (Zahlen ausgedacht). Beim Elektron im Grundzustand ist es dasselbe.
Das sind interessante und schwierige Fragen. Ob du eine befriedignede Antwort bekommst ist unwahrscheinlich ;-)
Die kinetische Energie ist zu einem bestimmten Bereich unbestimmt. D.h. es besitzt sozusagen mehrer kinetische Energien gleichzeitig.Peter0167 schrieb:Elektronen scheinen sich innerhalb eines Orbitals nicht zu bewegen!? Das würde ja bedeuten, dass sie keine kinetische Energie mehr besitzen, sondern nur noch potentielle Energie gemäß ihrer Position im elektrischen Feld.
Genauso ist auch der Ort nicht bestimmt. Man könnte flapsig sagen: Das Elektron ist gleichzeitig an verschiedenen Orten mit verschiedenen Geschwindigkeiten. Am besten ist es man verabschiedet sich von der Vorstellung von einem punktförmigen Etwas.
Orbitale selbst sind quasi das Elektron.Peter0167 schrieb:Elektronen scheinen sich innerhalb eines Orbitals nicht zu bewegen!?
Stell dir dazu den Doppelspaltverusch vor mit einzelnen Elektronen. Bevor das Elektron an einem bestimmten Detektorpunkt aufkommt, ist es zuvor verschmiert an allen Orten gleichzeitig, allerdings mit verschiedenen Gewichtungen: An manchen Stellen ist das "Elektron" z.B. nur zu 20 % an andere zu 60 % (Zahlen ausgedacht). Beim Elektron im Grundzustand ist es dasselbe.