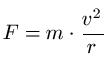Wie viel Newton liegen bei 6000U/min bei einer 150mm Scheibe an?

Moin

Mich würde mal interessieren wie viel Newton außen an einer Scheibe mit 150mm Durchmesser anliegen wenn sie sich mit 6000 U/min dreht?

Oder anders gefragt wie viel bar sind es?

Experimental Setup
The core of our setup is a rotating ring inside a large cryostat. Several
rings have been used so far including Niobium and Aluminum to test a
classical low-temperature superconductor as well as a non-superconductor
material for reference purposes (outer diameter of 150mm, wall thickness


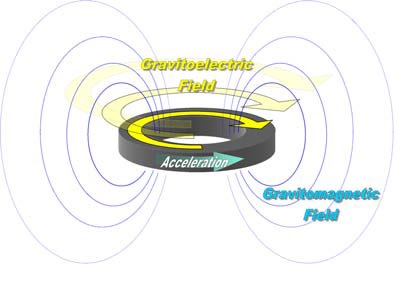
Figure 1: Gravitomagnetic and Gravitoelectric
Field Generated by a Rotating
and Angularly Accelerated Superconductor.


of 6mm and a height
of 15 mm), and a YBCO
high-temperature superconductor
(outer
diameter of 160mm and
wall thickness of 15 mm).
The ring can be rotated
using a brushless servo
motor or a pneumatic
air motor to minimize
any electromagnetic influence.
According to
the theoretical concepts,
a frame-dragging-like
field should be produced
directly proportional to
the superconductor’s
angular velocity. Another
aspect of Einstein’s theory is that a time-varying frame-dragging
field should give rise to non-Newtonian gravitational fields, also called
accelerational frame-dragging. Therefore, any angular acceleration of
the superconductor should produce a gravitational field along the ring’s
surface. A short illustration of the expected fields around the rotating
superconductor is shown in Fig. 1. Laser gyroscopes and low-noise
accelerometers can be used to detect those frame-dragging fields if they
are rigidly fixed to avoid any mechanical movement.

http://www.earthtech.org/experiments/tajmar/papers/TAM%20-%20Search%20for%20Frame-Dragging-Like%20Signals%20Close%20to%20Spinning%20Superconductors.pdf (Archiv-Version vom 16.11.2010)

The Nb,
Al and stainless steel rings had an outer diameter of 150 mm, a wall thickness of 6 mm and a height of
15 mm, whereas the YBCO and TEFON had a slightly larger outer diameter of 160 mm.

http://iopscience.iop.org/1742-6596/150/3/032101/pdf/1742-6596_150_3_032101.pdf

Eine Maschine für die Antigravitation



Tajmars Maschine funktioniert anders. Von außen sieht sie unspektakulär aus: eine brusthohe, mit Sand gefüllte Holzkiste; darin eingebettet ist ein Vakuumbehälter, mit Stahlträgern an Boden und Decke der Kiste verankert. In dem Behälter dreht sich ein 150 Millimeter breiter Ring aus dem seltenen Metall Niob. Mit flüssigem Helium auf minus 270 Grad Celsius abgekühlt, wird der Ring supraleitend: Strom kann dann ohne Widerstand durch ihn hindurchfließen. Tajmar versetzt diesen Supraleiter mit einem Motor in Rotation – bei 6000 Umdrehungen pro Minute meldet eines der Messgeräte ein bizarres Signal: Demnach hätte es sich verdreht. Aber wie kann das sein? Das Gerät ist fest installiert. Wenn das gemessene Signal korrekt ist, dann hat Tajmar ein künstliches Gravitationsfeld der besonderen Art erzeugt – ausreichend stark, um einen Gegenstand zu bewegen.


http://www.pm-magazin.de/t/raumfahrt-kosmos/gravitation/antigravitation-gibt-es-sie-doch (Archiv-Version vom 21.10.2014)


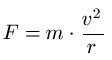
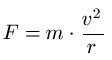
Zentrifugalkraft Formel 1:

Dabei ist:
•"F" die Fliehkraft in Newton [ N ]
•"m" die Masse in Kilogramm [ kg ]
•"v" ist die Geschwindigkeit in Meter pro Sekunde [ m/s ]
•"r" ist der Radius der Kreisbahn in Meter [ m ]

http://www.frustfrei-lernen.de/mechanik/fliehkraft.html

Dichte 8,57 g/cm3 (20 °C)[5]

Wikipedia: Niob

Zylinder Online berechnen

Werte für den Zylinder berechnet.

Radius: 75mm Umfang: 471.239mm
Höhe: 15mm Grundfläche: 17671.459
Mantelfläche: 7068.583
Oberfläche: 42411.501
Volumen: 265071.88

http://www.schulminator.com/mathematik/zylinder

Abzüglich der inneren Scheibe, wenn ich es mal so nennen darf.

Zylinder Online berechnen

Werte für den Zylinder berechnet.

Radius: 69mm Umfang: 433.54mm
Höhe: 15mm Grundfläche: 14957.123
Mantelfläche: 6503.097
Oberfläche: 36417.342
Volumen: 224356.839

http://www.schulminator.com/mathematik/zylinder

265071.88-224356.839 = 40715,041 mm³ = 40,715041 cm³

40,715041 cm³ * 8,57 g/cm³ = 348,92790137 Gramm =

471,239 / 348,92790137 = 1,350534016195805488216180136767 Gramm pro Millimeter Umfang

Jetzt haben wir 6000U/min und 471,239mm Umfang.

6000 U/min * 471,239 mm = 2827434mm/min = 2827,434 m/min = 47,1239m/Sek.

Jetzt haben wir eine Masse von 0,00135053401619580548821618013677 kg/mm Umfang.

0,00135053401619580548821618013677 kg/mm * 47,1239m/Sek. / 0,075m =

0,84856573234412690994867268196181 Newton je mm Umfang * 10 = 8,4856573234412690994867268196181 Newton je cm Umfang

1cm Umfang mal 1,5cm Höhe ist gleich = 1,5cm²

@Rattensohn

Dann haben wir p=F/A als Grundformel für den Druck
p: Der Druck
F: ist klar, die Kraft
A: Die Fläche -> 2cm²

Damit also p=27,8N/2cm²=13.9N/cm²=139000 N/m²

Die SI-Einheit von Druck ist Pascal (Pa) und 1Pa sind 1N/m²
Also haben wir p=139000Pa

Die Einheit Bar entspricht 10^5Pa
Womit dann p=1,39bar beträgt.

Wie könnte das Vril-Treibwerk funktionieren? (Seite 8)

8,4856573234412690994867268196181N / 1,5cm² = 5,6571048822941793996578178797454N / cm² = 0,56571 Bar

Liege ich mit den Newton und den Bar richtig oder ist das falsch?

Jetzt wäre noch interessant zu wissen, wie viel Newton oder Bar bei den ganzen Freien Energie Maschinen anliegt, z.B. der Repulsine, der Thestatika oder am Schumann Levitator! ;)

Die Repulsine jedenfalls musste sich erst mit 10.000U/min drehen um Energie zu erzeugen.

Geheimnis des Schuhmann Levitators

Die Flugkreisel des Viktor Schauberger



Tatsächlich hatte zum Beispiel der Klimator nur 60 cm Durchmesser.

Die von Viktor Schauberger auf eigene Kosten hergestellte Repulsine maß 65 cm im Durchmesser.

Von diesem Gerät wurden anscheinend mehrere Typen gebaut und an verschiedenen Orten vorgeführt. Er bestand aus einem Sockelteil, zwei Scheiben, einem Deckel und oben einem Aufsatz.
Zum Starten wurde ein schnell laufender Motor verwendet.
Zirka 10.000 bis 20.000 Umdrehungen pro Minute waren nötig, um den Levitations Prozess
mit Luft in Gang zu setzen.
Als Material wurde vornehmlich Kupfer und versilbertes Kupfer eingesetzt.

Nach Schaubergers Berrechnungen kann ein solches Gerät mit nur 20 cm Durchmesser bei
20.000 Upm etwa 228 Tonnen heben.

http://www.kheichhorn.de/html/body_flugkreisel.html


http://www.schulminator.com/mathematik/zylinder


Gehen wir jetzt mal davon aus, die Scheibe die rotiert, hat einen Durchmesser von 60cm und eine dicke von 2mm. Da in verschieden Bildern eher ein Wellen förmiges Blech zu sehen ist.

Bei einem Radius von 300mm und einer Dicke von 2mm würde der Umfang 1884.956mm betragen und das Volumen 565486.678mm³.

Wenn man die Scheibe auf den äußersten cm reduziert dann wäre es ein Voulmen von 565486.678 mm³ - 528415.884 mm³ = 37070,794 mm³ = 37,070794 cm³

Kupfer hat eine Dichte von 8,92 g/cm3 (20 °C)[5].

Wikipedia: Kupfer

37,070794 cm³ * 8,92/cm³ = 330,67148248 Gramm

Um das ganze wie bei der Niob Scheibe auf einen Vergleichs Wert zu stellen nehmen wir eine Wand-Dicke von 6mm.

Dann sind wir bei 198,402889488 Gramm.

Bei einer Geschwindigkeit von 10000U/min und einem Umfang von 1884,956mm wäre es eine Geschwindigkeit von 314,15933333333333333333333333333 Meter/Sek.

188,4956 cm / 198,402889488 Gramm = 0,95006479233459338054658281862654 Gramm/cm²

0,00095 kg/cm² * 314,15933333333333333333333333333 Meter/Sek. / 0,3m = 0,99483788888888888888888888888888N/cm² = 0,099 bar * doppelte Umdrehung(20000U/min) = 0,19896757777777777777777777777778 bar

Jetzt stellt sich mir die Frage ob die 2mm Stimmen bei 20mm hätten wir ja schon bar*10.

Öhm, ich hab mich verrechnet. Es sind ja nur 2mm dicke.

Dann das ganze mal 8 dann wären wir bei 7,958703111111111111111111111111 Newton am äußeren Rand und bei 0,79587 Bar bei 10.000U/min.

Und bei 20.000 U/min 1,5917406222222222222222222222222 Bar.

Bei einer 20cm Scheibe die angeblich 228 Tonnen heben kann wären es dann, 1,59174Bar/3=0,5305802074074074074074074074074 Bar.

Wohlgemerkt im Gegensatz zum Anti-Gravitations Experiment mit der Supraleitenden Niob Scheibe.

kp was du jetzt genau diskutieren willst ...
ist sowas nicht eher was für deinen blog ? ---> https://www.allmystery.de/blogs/Core-Spin

hmm ...
btw,

Core-Spin schrieb:Zentrifugalkraft Formel 1:

Dabei ist:
•"F" die Fliehkraft in Newton [ N ]
•"m" die Masse in Kilogramm [ kg ]
•"v" ist die Geschwindigkeit in Meter pro Sekunde [ m/s ]
•"r" ist der Radius der Kreisbahn in Meter [ m ]

wenns ein großes R wäre ...
aber so sieht mir das eher nach der zentripetalkraft aus .... ---> Wikipedia: Zentripetalkraft

Core-Spin schrieb:Jetzt wäre noch interessant zu wissen, wie viel Newton oder Bar bei den ganzen Freien Energie Maschinen anliegt, z.B. der Repulsine, der Thestatika oder am Schumann Levitator! ;)

Die Repulsine jedenfalls musste sich erst mit 10.000U/min drehen um Energie zu erzeugen.

repulsine? wtf?!?... das ist ein braunes esotherik/VT -phantasieprodukt.
hat und wird auch nie funktionieren...
was für eine energie sollte denn da bitte entstanden sein ? oO :ask: Oo ?



sollte das thread nicht eher in die rubrik VT ?
hmm...

@iwok

Dieses Anti-Grav Experiment scheint ja zu funktionieren.

Core-Spin schrieb:Dieses Anti-Grav Experiment scheint ja zu funktionieren.

was meinst du?
das mit den sich drehenden supraleitern?
hmm kp, ich hatte da mal vor jahren einen bericht im TV gesehen und vor einiger zeit wollte ich auch mal wieder wissen was sich da so neues ergeben hat ...
naja, ergeben hatte sich da nicht all zuviel, so wie ich das verstanden habe, konnte das bisher nicht wiederholt werden ...

allerdings gibt es zu dem thema hier im forum schon min. ein thread dazu ...

btw, das mit den supraleitern hätte für ein thread vollkommen ausgereicht. du packst da sehr viel in dein thread rein und das mit den reichsflugscheiben hat nun wirklich nichts in der rubrik hier zu suchen ....

@iwok

Es ging mir halt auch darum das man mit 1 Bar die Atome ausrichten können müsste.

Was hier diskutiert wurde:

Wie könnte das Vril-Treibwerk funktionieren?

Es ging mir halt auch darum das man mit 1 Bar die Atome ausrichten können müsste.

Was hier diskutiert wurde:

Diskussion: Wie könnte das Vril-Treibwerk funktionieren?

na dann diskutier das in dem entsprechenden thread, das du gepostet hast ;) und mach keine unnötigen "quer-threads" auf...

btw ---> Schlüsselwort: Antigravitation (17 threads .... da ist bestimmt so einiges auch mit supraleitern dabei .... )

@iwok

Zudem müssten sich die Atome zum Rand hin verdichten was einem Supraleitenden Effekt eventuell ähnlich kommen würde. :D

Weil Schauberger schrieb ja auch immer von Implosion und dort findet eine Verdichtung statt und er schrieb auch von einer Abkühlung der Atome.

Und Supraleitung ist ja Ultra Kalt.

Zudem wollte ich eine Hilfestellung zur Berechnung haben die ich aber anscheinend dann doch nicht brauchte.

Core-Spin schrieb:Zudem müssten sich die Atome zum Rand hin verdichten was einem Supraleitenden Effekt eventuell ähnlich kommen würde.

ehrm eigentlich nicht. supraleiter (SL) leiten elektr. strom mit so geringem widerstand, dass man diesen quasi vernachlässigen kann. ganz nebenbei treten da relativ ungewöhnliche* effekte auf, beispielsweise kann man einen supraleiter in einem magnetischen feld schweben, relativ mühelos (der SL muss halt ständig sehr kalt sein) schweben lassen...

*ungewöhnlich, da man es nicht jeden tag sieht ...

Core-Spin schrieb:Weil Schauberger schrieb ja auch immer von Implosion und dort findet eine Verdichtung statt und er schrieb auch von einer Abkühlung der Atome.

wer ist das und was hat der geschrieben ?

Core-Spin schrieb:Und Supraleitung ist ja Ultra Kalt.

ein bose-einstein-kondensat (aggregatzustand) ist ultrakalt (ultratiefe temperaturen).
bei supraleitern versucht man ständig die temperatur, bei der das material supraleitend ist, zu erhöhen ...
soweit ich weiß ist man da irgendwo so bei ca. -150°C. das ist zwar kalt, aber nicht "ultra" ...


achja und VRIL ist doch auch so ein brauner esomüll / VT ....

@Core-Spin

Was hast du denn da gemacht?

265071.88-224356.839 = 40715,041 mm³ = 40,715041 cm³

40,715041 cm³ * 8,57 g/cm³ = 348,92790137 Gramm =

471,239 / 348,92790137 = 1,350534016195805488216180136767 Gramm pro Millimeter Umfang

Das ist doch quatsch. Die Dichte ist im ganzen Material die gleiche.


Kurzer Überschlag:

Dichte.................rho = 8570 kg/m³
Radius................r = 0,075 m
Höhe..................h = 0,015 m
Umfang..............U = 0,471 m (= 2*pi*r)
Geschwindigkeit...v = 47,1 m/s (= Rotation*Umfang)
Volumen.............V = 0.00027 m (= pi*r²*h)
Masse................m = 2,3625 kg (= rho*V)
Grundfläche........G = 0,018 m (= pi*r²)

Zentipetalkraft (wirkt nach innen):
F = m *v²/r

F = (2,3625 kg * 47,1² m²/s²) / 0,075 m = 69880 kg*m/s² = 69880 N

Druck: P = F/U = (69880 N / 0,471 m * 0,015m) = 493,7 N/m² = 0,004937 bar

Also nach meiner Rechnung ist die Zentripetalkraft in der Scheibe (egal wo in der Scheibe, da ist es egal ob du außen bist oder innen, die Kraft ist überall gleich) 69880 N.

Und der Druck der von außen auf die Scheibe wirkt ist 0,004937 bar.

Da bin ich etwas geringer als du... aber ich bin sicher, das ich mich nicht verrechnet habe.

Mit 2 mm Höhe kommt dann folgendes raus:

Dichte.................rho = 8570 kg/m³
Radius................r = 0,075 m
Höhe..................h = 0,002 m
Umfang..............U = 0,471 m (= 2*pi*r)
Geschwindigkeit...v = 47,1 m/s (= Rotation*Umfang) [6000 U/min]
Volumen.............V = 0.000035 m (= pi*r²*h)
Masse................m = 0,3 kg (= rho*V)
Grundfläche........G = 0,018 m (= pi*r²)
Kraft...................F = 4 N
Druck..................P = 0,04246 bar

@Core-Spin

Core-Spin schrieb:Zudem müssten sich die Atome zum Rand hin verdichten

Aber nur wenn du sehr-sehr weiches Material nimmst. Das bisschen Beschleunigung erzeugt zwar Druck, aber keine Verformungen. Sonst gäbs bei allem das sich dreht (Motoren, Festplatten ...) große Probleme.

@Core-Spin

Core-Spin schrieb:bei 6000 Umdrehungen pro Minute meldet eines der Messgeräte ein bizarres Signal: Demnach hätte es sich verdreht. Aber wie kann das sein? Das Gerät ist fest installiert. Wenn das gemessene Signal korrekt ist, dann hat Tajmar ein künstliches Gravitationsfeld der besonderen Art erzeugt

Du darfst nicht alles glauben, was du im PM-Magazin liest ;)

"Tajmar behauptete, in seinen Experimenten mit schnell rotierenden Supraleitern aus Niob ein Äquivalent zum Magnetismus für Gravitation nachgewiesen zu haben.[15][16] Daher wurde über diese Arbeiten in überregionalen Medien berichtet.[17][18][19] Der gemessene gravito-magnetische Effekt schien um viele Größenordnungen größer zu sein, als nach der bekannten Theorie des Lense-Thirring-Effekts zu erwarten war (Faktor 10^18 ). Tajmar hat auch eine Theorie des behaupteten Effekts entwickelt;[20][21] diese wurde an der University of Canterbury, Neuseeland, in einem ähnlichen Experiment mit einem rotierenden Zylinder aus supraleitendem Blei und Laser-Gyroskopen widerlegt. Eine von Tajmar später behauptete Paritätsverletzung [22] oder andere Theorien[23] können dadurch jedoch nicht ausgeschlossen werden.[24][25][26][27][28] Neuere Arbeiten von Tajmar deuten auf eine Fehlinterpretation seiner Messresultate hin. Möglicherweise beeinflusste das zur Kühlung verwendete flüssige Helium die Messapparatur.[29]"
Wikipedia: Martin Tajmar

geeky schrieb:Du darfst nicht alles glauben, was du im PM-Magazin liest ;)

Was bleibt ihm dann noch? Gott? Das Internet? Sein eigenes Gehirn? Oje.

Kurzer Überschlag:

Dichte.................rho = 5520 kg/m³
Radius................r = 6371 m
Höhe..................h = ???
Umfang..............U = 40030.174 m (= 2*pi*r)
Geschwindigkeit...v = 66850100 m/s (= Rotation*Umfang)

Um genau zu sein: Am Äquator beträgt der Erdradius etwa 6.378 Kilometer, man kommt also auf einen Umfang von rund 40.075 Kilometern und somit auf einen Geschwindigkeit von 1.670 Kilometern pro Stunde
http://www.wasistwas.de/wissenschaft/eure-fragen/erde/link//be69a84cc3/article/wie-schnell-dreht-sich-die-erde-eigentlich.html?tx_ttnews

Volumen.............V = 1.083.319.780.000, km³ (= pi*r²*h)
Masse................m = 5,972E24 kg (= rho*V) =5970000000000000000000000kg
Grundfläche........G = ??? (= pi*r²)

Zentipetalkraft (wirkt nach innen):
F = m *v²/r

F = (5970000000000000000000000kg * 66850100² m²/s²) / 6371 m = 4,1876545509275937843352691885104e+36 kg*m/s² = 4,1876545509275937843352691885104e+36 N

Druck: P = F/U = (4,1876545509275937843352691885104e+36 N / 40030.174 m) = 493,7 N/m² = 1,046124493720060718280982038327e+32 bar

@Schdaiff

Ich hab deine Rechnung mal mit der Rechnung der Erde ergänzt und irgendwie scheint mir das ganze komisch zu sein oder hab ich mich da irgendwo vertan?

Ich kann mir nicht vorstellen das dort ein Druck von 1,046124493720060718280982038327e+32 Bar herrschen soll????

@Core-Spin

Core-Spin schrieb:Radius................r = 6371 m

Also 6,3km?

Core-Spin schrieb:Umfang..............U = 40030.174 m

Also ~40km?

Von welchen Objekt redest du eigentlich?

Core-Spin schrieb:Geschwindigkeit...v = 66850100 m/s (= Rotation*Umfang)

Das sind dann ~70.000km/s oder 22% der Lichtgeschwindigkeit.

Core-Spin schrieb:und somit auf einen Geschwindigkeit von 1.670 Kilometern pro Stunde

Das stimmt Ausnahmsweise. Das sind dann übrigens ~460m/s.

Zentipetalkraft ...
F = m *v²/r
F = (5970000000000000000000000kg * 66850100² m²/s²) / 6371 m =

Du hast das falsche m, das falsche v und das falsche r. Die gute Nachricht: die Formel ist die Korrekte. (Obwohl, ich hab keine Ahnung was du da berechnen willst. Also ist die u.U. auch falsch.)

@TTucker

Danke für deine Hilfe! Ich rede von der Erde hab mich da ein wenig vertan. :D

Ne 6371km :D

Wie wäre es denn korrekt für die Erde? In Bar?

ich wollte eigentlich die Zentrifugalkraft wissen aber da wie hier steht diese gleich groß sind spielt das keine Rolle.

Im Sinne des dynamischen Gleichgewichts ist die Zentrifugalkraft stets entgegengesetzt gleich groß wie die Zentripetalkraft.
Wikipedia: Zentrifugalkraft

@Core-Spin

Core-Spin schrieb:Wie wäre es denn korrekt für die Erde? In Bar?

Ich hab keine Ahnung was du da Rechnen willst. Also ist selber machen angesagt.

@TTucker

Ich will den Druck ausrechnen, der auf die Erde durch die Zentrifugalkraft wirkt. Und das ganze am besten in Bar.

@Core-Spin
Zentrifugal oder Zentripetal?